Mathématiques,
Brevet des collèges Amérique du sud 2014
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1. QCM.
1.
Une école de musique organise un concert de fin d’année. Lors de cette
manifestation la recette s’élève à 1 300 €. Dans le public il y a 100
adultes et 50 enfants. Le tarif enfant coûte 4 € de
moins que le tarif adulte. Le tarif enfant est :
10 € ; 8 € ; 6 €.
On note x le tarif enfant : 50 x +100(x+4)=1300 ;
150 x +400 = 1300 ; 150 x = 900 ; x = 900 / 150 = 6.
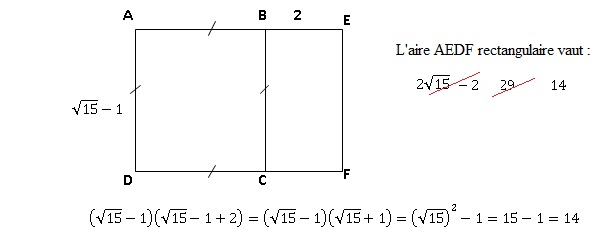
2. 
3. Le 27 janvier
2012, peu avant 16 h, un séisme de magnitude 5,4 s’est produit dans la
province de Parme dans le nord de l’Italie. La secousse a été ressentie
fortement à Gênes, Milan, Turin mais également dans une moindre mesure
à Cannes dans les Alpes Maritimes.
Les ondes sismiques ont mis 59 secondes pour parvenir à Cannes, située
à 320 km de l’épicentre.
La vitesse de propagation des ondes sismiques, exprimée en kilomètres
par seconde, arrondie au dixième, est :5,4
; 10,8 ; 59,3.
320 / 59 = 5,4 km /s.
Exercice
2.
On considère le parallélépipède rectangle ABCDEFGH.
M est un point de [FG] et N un point de [EF].
On donne : FE = 15 cm; FG = 10 cm; FB = 5 cm; FN = 4 cm; FM= 3 cm.
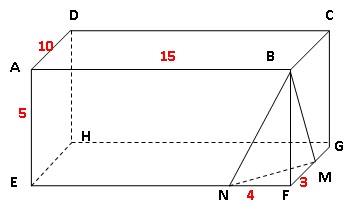
1. Démontrer que
l’aire du triangle FNM est égal à 6 cm2.
base x hauteur / 2 = NF x FM / 2 = 4 x 3 / 2 = 6 cm2.
2. Calculer le
volume de la pyramide de sommet B et de base le triangle FNM.
Base triangulaire x hauteur / 3 = 6 x5 /3 = 10 cm3.
3. On considère le
solide ABCDENMGH obtenu en enlevant la pyramide précédente au
parallélépipède rectangle.
a. Calculer son
volume.
Volume du parallélépipède rectangle : AB x AD xAE =10 x 15 x 5 = 750 cm3.
750-10 = 740 cm3.
b. On appelle
caractéristique d’Euler d’un solide le nombre x tel que :
x = nombre de faces−nombre d’arêtes+nombre de sommets. Recopier et
compléter le tableau suivant :
|
Parallélépipède
ABCDEFGH
|
Solide
ABCDENMGH
|
Nombre
de faces
|
6
|
7
|
Nombre
d'arètes
|
12
|
14
|
Nombre
de sommets
|
8
|
9
|
Caractéristique
x
|
2
|
2
|
.
|
| ... |
|
|
Exercice 3.
Le
document ci-dessous indique les tarifs postaux pour un envoi depuis la
France métropolitaine d’une lettre ou d’un paquet en mode « lettre
prioritaire ».
Ces tarifs sont fonction du poids de la lettre.
• Pour les envois vers : La France,
Monaco, Andorre et secteurs postaux (armée).
Complément d’affranchissement aérien vers l’Outre-mer pour les envois
de plus de 20 g
• Service universel : Jusqu’à 2 kg
• Délai : J + 1, indicatif
• Dimensions : Minimales : 14×9 cm, maximales : L + l + H = 100 cm,
avec L < 60 cm
• Complément aérien :
- Vers zone OM1 : Guyane, Guadeloupe, Martinique, La Réunion, St Pierre
et Miquelon, St-Barthélémy, St-Martin et Mayotte : 0,05 ( par tranche
de 10 g).
- Vers zone OM2 : Nouvelle-Calédonie, Polynésie française, Wallis-et
Futuna, TAAF. : 0,11 ( par tranche de 10 g).
• Exemple de complément : Pour un envoi de 32 g vers la Guadeloupe :
1,10€ ++ 4×0,05€= 1,3 €.
Poids
jusqu'à
|
20g
|
50g
|
100g
|
250g
|
500g
|
1
kg
|
2
kg
|
3
kg
|
tarif
net ( €)
|
0,66
|
1,10
|
1,65
|
2,65
|
3,55
|
4,65
|
6,00
|
7,00
|
1.
Expliquer pourquoi le coût d’un envoi vers la France Métropolitaine, en
« lettre
prioritaire », d’une lettre de 75 g est de 1,65 €.
Le poids est compris entre 50 et 100 g ; envoi vers la métropole : 1,65
€.
2. Montrer que le
coût d’un envoi à Mayotte, en « lettre prioritaire », d’une lettre de
109 g est de 3,20 €.
Tarif pour une lettre de poids inférieure à 250 g : 2,65 €.
Complément aérien zone OM1 : 11 x 0,05 = 0,55 €.
Total : 2,65 +0,55 = 3,20 €.
3. Au moment de
poster son courrier à destination de Wallis-et-Futuna, Loïc s’aperçoit
qu’il a oublié sa carte de crédit et qu’il ne lui reste que 6,76 € dans
son porte-monnaie.
Il avait l’intention d’envoyer un paquet de 272 g, en « lettre
prioritaire ». Peut-il payer le montant correspondant ?
Tarif
pour une lettre de poids inférieure à 500 g : 3,55 €.
Complément aérien zone OM2 : 28 x 0,11 = 3,08 €.
Total : 3,55 +3,08 = 6,63 €. Il peut payer.
4.
Le paquet a les dimensions suivantes : L = 55 cm l = 30 cm et h = 20
cm. Le guichetier de l’agence postale le refuse. Pourquoi ?
:
L + l + H =55 + 30 +20 = 105 cm, valeur supérieure à 100 cm, donc refus.
Exercice 4.
Le
principe d’un vaccin est d’inoculer (introduire dans l’organisme) à une
personne saine, en très faible quantité, une bactérie, ce qui permet à
l’organisme de fabriquer des anticorps. Ces anticorps permettront de
combattre la maladie par la suite si la personne souffre de cette
maladie.
Lors de la visite médicale de Pablo le jeudi 16 octobre, le médecin
s’aperçoit qu’il n’est pas à jour de ses vaccinations contre le
tétanos. Il réalise alors une première injection d’anatoxine tétanique
et lui indique qu’un rappel sera nécessaire. On réalise des prises de
sang quotidiennes pour suivre la réaction de l’organisme aux injections.
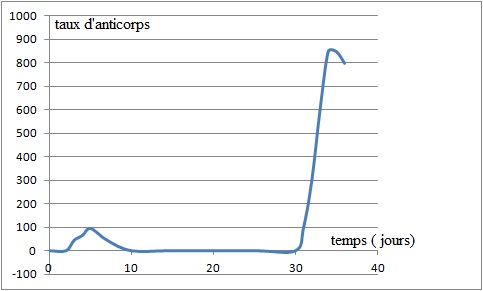
1. Combien de jours
faut-il attendre, après la première injection, pour constater une
présence d’anticorps ?
Unefaible présence d'anticorps est constater 2 jours après
l'injection.
2. Quelle est la
valeur maximale du taux d’anticorps atteinte après la première
injection?
A quel jour de la semaine correspond cette valeur ?
Mardi 21 octobre, le taux d'anticorps est voisin de 100.
3. Au bout de
combien de jours approximativement, après la première injection, Pablo
n’a t-il plus d’anticorps dans son organisme ?
10 jours plus tard.
4. Durant combien
de jours environ le taux d’anticorps est supérieur à 800 ?
Environ 2 jours.
|
|
|
|
Exercice 5.
L’oncle de Pauline participe régulièrement à une
régate* organisée tous les ans sur le même plan d’eau.
* régate : course de voiliers.
En 2012, il a réalisé le parcours constitué de deux boucles courtes et
de trois boucles longues en 8 heures et 40 minutes.
Lors de sa participation en 2013, il lui a fallu 8 heures et 25 minutes
pour achever le parcours constitué, cette année-là, de trois boucles
courtes et de deux boucles longues.
Il se souvient qu’il n’a parcouru aucune boucle en moins de 75 minutes.
Il sait aussi qu’il lui a fallu, pour parcourir la boucle longue, 15
minutes de plus que pour la boucle courte.
Cependant il souhaite connaître la durée nécessaire pour parcourir sur
son voilier la boucle courte et la boucle longue.
1. Convertir en
minutes les temps réalisés pour ces parcours de 2012 et 2013.
8 h 40 min = 8 x60 +40 = 520 min ; 8 h 25 min = 8 x60 +25 = 505 min.
2. Pauline a
décidé, en utilisant un tableur, d’aider son oncle à déterminer les
durées pour la boucle courte ainsi que pour la boucle longue.
Une copie de l’écran obtenu est donnée ci-dessous.
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
1
|
x
|
75
|
80
|
85
|
90
|
95
|
100
|
2
|
f(x)
|
90
|
95
|
100
|
105
|
110
|
115
|
3
|
f(x)
|
420
|
445
|
470
|
495
|
520
|
545
|
4
|
f(x)
|
405
|
430
|
455
|
480
|
505
|
530
|
|
|
|
|
|
|
|
|
Elle a noté x la durée en minutes pour la boucle courte.
a. Quelle formule
permettant d’obtenir la durée en minutes nécessaire au parcours de la
boucle longue va-t-elle saisir dans la cellule B2 ?
= B1+15
b. Elle va saisir
dans la cellule B3 la formule « =2*B1+3*B2 ». Que permet de calculer
cette formule ?
La durée du parcours 2012.
c. Quelle formule
va-t-elle saisir dans la cellule B4 pour calculer le temps de parcours
lors de sa participation en 2013 ?
=3*B1+2*B2
Elle a ensuite recopié vers la droite les formules saisies en B2, B3 et
B4.
3. Si elle saisit
le nombre 105 dans la cellule H1, quelles valeurs obtiendra-t-elle dans
les cellules H2, H3 et H4 ?
H2 : 105+15 = 120 ; H3 : 2 x105 +3 x120 = 570 ; H4 : 3 x105 + 2x120 =
555.
4. À l’aide de la
copie de l’écran obtenu avec le tableur préciser les durées nécessaires
à son oncle pour parcourir la boucle courte ainsi que pour parcourir la
boucle longue.
Colonne F : 95 min pour la boucle courte et 110 minutes pour la boucle
longue.
Exercice 6.
Lors
d’une activité sportive, il est recommandé de surveiller son rythme
cardiaque. Les médecins calculaient autrefois, la fréquence cardiaque
maximale recommandée fm exprimée en battements par minute,
en soustrayant à 220 l’âge a de la personne exprimé en années.
1. Traduire cette
dernière phrase par une relation mathématique.
fm = 220-a, avec a âge de la personne .
2. Des recherches
récentes ont montré que cette relation devait être légèrement modifiée.
La nouvelle relation utilisée par les médecins est :
Fréquence cardiaque maximale recommandée = 208−(0,75×a).
a. Calculer la
fréquence cardiaque maximale à 60 ans recommandée aujourd’hui par les
médecins.
208-0,75 x60 = 163.
b. Déterminer l’âge
pour lequel la fréquence cardiaque maximale est de 184 battements par
minute.
184 = 208-0,75 a ; 208-184 = 0,75 a ; 24 = 0,75 a ; a = 24 / 0,75 = 32
ans.
c. Sarah qui a
vingt ans court régulièrement. Au cours de ses entraînements, elle
surveille son rythme cardiaque.
Elle a ainsi déterminé sa fréquence cardiaque maximale recommandée et a
obtenu 193 battements par minute. Quand elle aura quarante ans, sa
fréquence cardiaque maximale sera de 178 battements par minute.
Est-il vrai que sur cette durée de vingt ans sa fréquence cardiaque
maximale aura diminué d’environ 8%?
(193-178 ) / 193 = 0,078 ( 7,8 %). C'est vrai.
|
|
Exercice 7.
Joachim
doit traverser une rivière avec un groupe d’amis. Il souhaite installer
une corde afin que les personnes peu rassurées puissent se tenir. Il
veut connaître la largeur de la rivière à cet endroit (nommé D) pour
déterminer si la corde dont il dispose est assez longue. Pour cela il a
repéré un arbre (nommé A) sur l’autre rive.
Il parcourt 20 mètres sur la rive rectiligne où il se situe et trouve
un nouveau repère : un rocher (nommé R).
Ensuite il poursuit sur 12 mètres et s’éloigne alors de la rivière, à
angle droit, jusqu’à ce que le rocher soit aligné avec l’arbre depuis
son point d’observation (nommé B).
Il parcourt pour cela 15 mètres. Il est alors satisfait : sa corde
d’une longueur de 30 mètres est assez longue pour qu’il puisse
l’installer entre les points D et A.
A l’aide de la figure, confirmer sa décision.
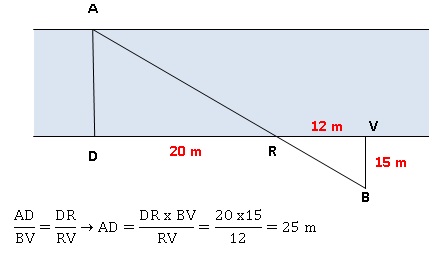
|
|