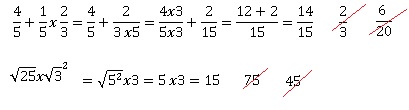
Mathématiques, Brevet des collèges Nlle Calédonie 2014 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Exercice 1.  QCM. Combien font 5 % de 650 ? 32,5 ; 645 ; 13000. 650 x0,005 = 32,5. Quelle est approximativement la masse de la terre ? 32 tonnes ; 6 x 1024 kg ; 7 x 10-15 g. . . Exercice 2. Dans le jeu pierre–feuille–ciseaux deux joueurs choisissent en même temps l’un des trois « coups » suivants : pierre en fermant la main feuille en tendant la main ciseaux en écartant deux doigts -La pierre bat les ciseaux (en les cassant). - Les ciseaux battent la feuille (en la coupant). - La feuille bat la pierre (en l’enveloppant). - Il y a match nul si les deux joueurs choisissent le même coup (par exemple si chaque joueur choisit « feuille »). 1. Je joue une partie face à un adversaire qui joue au hasard et je choisis de jouer « pierre ». a. Quelle est la probabilité que je perde la partie ? Seule la feuille peut battre la pierre, soit un cas favorable sur 3 cas possibles. La probabilité de perdre  est 1/3. b. Quelle est la probabilité que je ne perde pas la partie ? 1-1 /3 = 2 / 3. 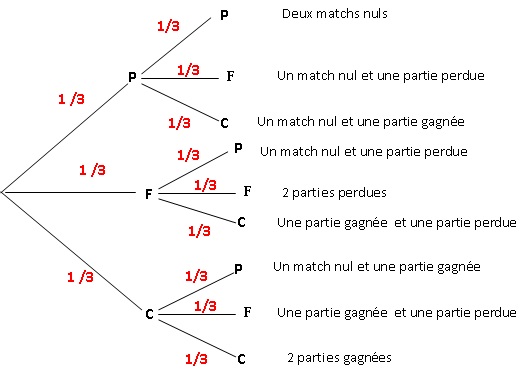2. Je joue deux parties de suite et je choisis de jouer « pierre » à chaque partie. Mon adversaire joue au hasard. Construire l’arbre des possibles de l’adversaire pour ces deux parties. On notera P, F, C, pour pierre, feuille, ciseaux. 3. En déduire : a. La probabilité que je gagne les deux parties. 1 / 9. b. La probabilité que je ne perde aucune des deux parties.4 / 9 ... Exercice 3. 1. a. Construire un triangle ABC isocèle en A tel que AB = 5 cm et BC = 2 cm. b. Placer le point M de [AB] tel que BM= 2 cm. c. Tracer la parallèle à [BC] passant par M. Elle coupe [AC] en N. 2. Calculer les longueurs MN et AN en justifiant. 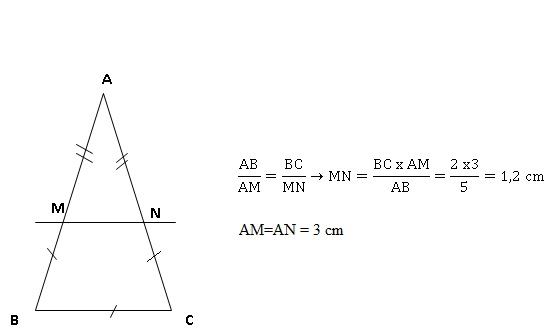3. Montrer que les périmètres du triangle AMN et du quadrilatère BMNC sont égaux. Périmètre du triangle :2AM +Mn = 2 x3 +1,2 = 7,2 cm. Périmètre du quadrilatère : 3 BC +MN = 3 x2 +1,2 = 7,2 cm. Exercice 4. Mathilde et Eva se trouvent à la Baie des Citrons. Elles observent un bateau de croisière quitter le port de Nouméa. Mathilde pense qu’il navigue à une vitesse de 20 noeuds. Eva estime qu’il navigue plutôt à 10 noeuds. Elles décident alors de déterminer cette vitesse mathématiquement. Sur son téléphone, Mathilde utilise d’abord la fonction chronomètre. Elle déclenche le chronomètre quand l’avant du navire passe au niveau d’un cocotier et l’arrête quand l’arrière du navire passe au niveau du même cocotier ; il s’écoule 40 secondes. Ensuite, Eva recherche sur Internet les caractéristiques du bateau. Voici ce qu’elle a trouvé : Caractéristiques techniques : Longueur : 246 m Largeur : 32 m Calaison : 6 m Mise en service : 1990 Nombre maximum de passagers : 1 596 Membres d’équipage : 677 1. Quelle distance a parcouru le navire en 40 secondes ? 246 m. 2. Qui est la plus proche de la vérité,Mathilde ou Eva ? Justifier la réponse. Rappel : Le « noeud » est une unité de vitesse. Naviguer à 1 noeud signifie parcourir 0,5 mètre en 1 seconde. 246 / 40 = 6,15 m /s soit 6,15 x2 = 12,3 noeuds. Eva a raison. . . Exercice 5. Le tableau ci-dessous présente l’évolution des températures minimales (Tmin) et des températures maximales (Tmax) observées en différents endroits de la Nouvelle- Calédonie au cours des quarante dernières années : Nouméa Vaté Thio Nessadiou Houatlou Poindimié Koné Koumac La Roche Ouanaham Tmin °C 1,3 1,3 1,2 1,2 1,2 1,3 1,2 1,2 1,5 1,3 Tmaxi °C 1,3 1,3 1,0 0,9 1,0 1,0 0,8 0,9 1,0 0,9 1. Les informations de ce tableau traduisent-elles une augmentation des températures en NouvelleCalédonie ? Justifier. Toutes les valeurs sont positives : les températures augmentent. 2. En quel endroit la température minimale a-t-elle le plus augmenté ? La Roche. 3. Calculer l’augmentation moyenne des températures minimales et celle des températures maximales. Hausse moyenne des températures minimales  : (1,3 +1,3 +1,2 +1,2 +1,2 +1,3 +1,2 +1,2 +1,5 +1,3) / 10 =1,27°C. Hausse moyenne des températures maximales : (1,3 +1,3 +1,0 +0,9 +1 +1 +0,8 +0,9 +1 +0,9) / 10 =1,0°C. Exercice 6. Les éoliennes sont construites de manière à avoir la même mesure d’angle entre chacune de leurs pales. 1. Une éolienne a trois pales. Quelle est la mesure de l’angle entre deux de ses pales ? 360 / 3 = 120° 2. Pour réduire le bruit provoqué par les éoliennes, il faut augmenter le nombre de pales. On a représenté le mât d’une éolienne à six pales par le segment [AB]. En prenant le point A pour centre des pales, compléter la construction avec des pales de 5 cm. 3. On estime qu’à 80 m du centre des pales d’une éolienne le niveau sonore est juste suffisant pour que l’on puisse entendre le bruit qu’elle produit. Un randonneur dont les oreilles sont à 1,80 m du sol se déplace vers une éolienne dont le mât mesure 35 m de haut. Il s’arrête dès qu’il entend le bruit qu’elle produit. 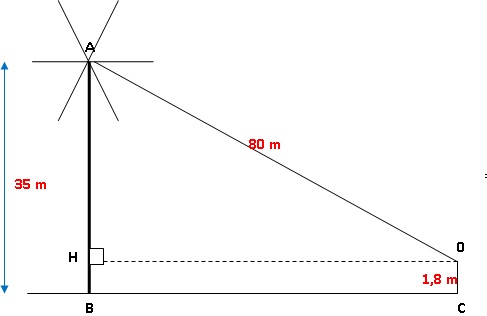À quelle distance du mât de l’éolienne (distance BC) se trouve-t-il ? Arrondir le résultat à l’unité. OH2 = OA2 -AH2 = 802 -(35-1,8)2 =5297,76 ; OH = BC ~73 m. Exercice 7. À l’aide d’un tableur, on a réalisé les tableaux de valeurs de deux fonctions dont les expressions sont : f (x) = 2x et g (x) = −2x +8. B2 =2*B1 A B C D E F 1 valeur de x 0 1 2 3 4 2 image de x 0 2 4 6 8 3 4 valeur de x 0 0,5 1 2 4 5 Image de x 8 7 6 4 0 1. Quelle est la fonction ( f ou g ) qui correspond à la formule saisie dans la cellule B2 ? f(x) ; formule saisie en B2 : =2B1 2. Quelle formule a été saisie en cellule B5 ? =-2*B4+8 3. Laquelle des fonctions f ou g est représenté ci dessous ? 4. Tracer la représentation graphique de la deuxième fonction dans ce repère. 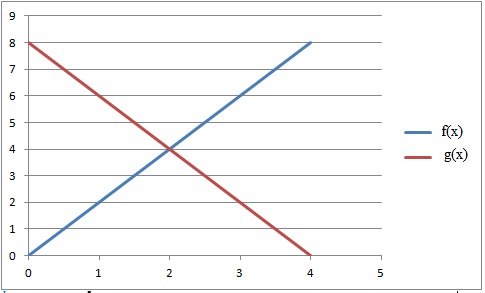5. Donner, en justifiant, la solution de l’équation : 2x = −2x +8. Abscisse du point dl'intersection des deux droites : x = 2. Exerciice 8. Le dépit de carburant de Koumourou, à Ducos, dispose de trois sphères de stockage de butane. 1. La plus grande sphère du dépôt a un diamètre de 19,7 m. Montrer que son volume de stockage est d’environ 4 000 m3. 4 / 3 p R3 = 4 / 3 *3,14 (19,7 / 2)3 4003 ~4000 m3. 2. Tous les deux mois, 1 200 tonnes de butane sont importées sur le territoire. 1 m3 de butane pèse 580 kg. Quel est le volume, en m3, correspondant aux 1 200 tonnes ? Arrondir le résultat à l’unité. 1200 x 103 / 580 ~2069  m3. 3. Les deux plus petites sphères ont des volumes de 1 000 m3 et 600 m3. Seront elles suffisantes pour stocker les 1 200 tonnes de butane, ou bien aura-t-on besoin de la grande sphère ? Justifier la réponse. Le volume total des deux petites sphères est de 1600 m3, valeur inférieure à 2069. Il faudra utiliser également la grande sphère.

menu