Mathématiques,
Brevet des collèges Amérique du Nord 2015
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1.
Cet exercice est un QCM(questionnaire à choix multiples). Pour chaque
ligne du tableau, une seule affirmation est juste.
Sur votre copie, indiquer le numéro de la question et recopier
l’affirmation juste. On ne demande pas de justifier.
|
Questions
|
A
|
B
|
C
|
1
|
Quelle
est l'écriture scientifique de
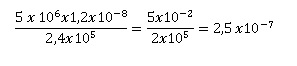
|
25
x10-8
faux
|
2,5 x 10-7 Vrai
|
2,5
103 Faux.
|
2
|
Pour
x = 20 et y = 5 quelle est la valeur de R dans l'expression :
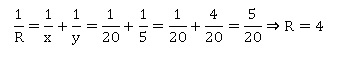
|
0,25
Faux
|
4 Vrai
|
25
Faux
|
3
|
Un
article coûte 120 €. Une fois soldé, il coûte 90 €. Quel est le
pourcentage de réduction ?
(120-90) / 120 x 100 = 25 %
|
25 % Vrai
|
30
% Faux
|
75%
Faux
|
4
|
On
considère l'agrandissement de coefficient 2 d'un rectangle ayant pour
largeur 5 cm et pour longueur 8 cm. Quelle est l'aire du rectangle
obtenu ?
2 x5 x2 x8 = 160 cm2
|
40
cm2 Faux
|
80
cm2 Faux
|
160 cm2 Vrai.
|
Exercice 2.
Lors d’une étape cycliste, les distances parcourues par un cycliste ont
été relevées
chaque heure après le départ. Ces données sont précisées dans le
graphique ci-dessous :
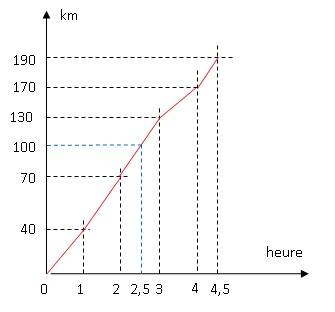
1. a. Quelle est
la distance totale de cette étape ?
190 km.
b. En combien de
temps le cycliste a-t-il parcouru les cent premiers kilomètres ?
2,5 h = 2 h 30 min.
c. Quelle est la
distance parcourue lors de la dernière demi-heure de course ?
190-170 = 20 km.
2. Y-a-t-il
proportionnalité entre la distance parcourue et la durée de parcours de
cette étape ?
Justifier votre réponse et proposer une explication.
Non, durant la première heure, la distance parcourue est 40 km ; durant
l'heure suivante, la distance parcourue est 30 km. Durant la troisième
heure la distance parcourue est 50 km.
Le graphe n'est pas une droite passant par l'origine ; la vitesse n'est
pas constante.
|
| ... |
|
|
Exercice 3.
On
lance deux dés tétraédriques, équilibrés et non truqués, dont les faces
sont numérotées de 1 à 4. On calcule la somme des nombres lus sur
chacune des faces sur lesquelles reposent les dés.
1 000 lancers sont simulés avec un tableur. Le graphique suivant
représente la fréquence d’apparition de chaque somme obtenue :
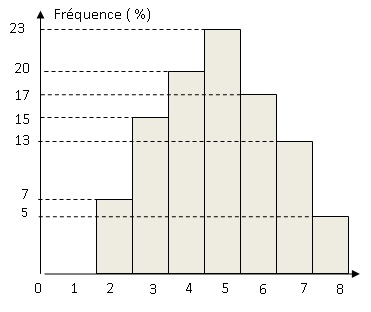
1. Par lecture graphique donner la
fréquence d’apparition de la somme 3.
15 %.
2. Lire la
fréquence d’apparition de la somme 1 ? Justifier cette fréquence.
Chaque dé est numéroté de 1 à 4 et on lance deux dés. La plus
petite somme est donc 2. La fréquence d'apparition de 1 est nulle.
3. a. Décrire les
lancers de dés qui permettent d’obtenir une somme égale à 3.
L'un des dés indique 1 et l'autre 2. Deux cas permettent d'obtenir la
somme 3.
Le dé n°1 indique 1 et le dé n°2 indique 2.
Le
dé n°1 indique 2 et le dé n°2 indique 1.
b. En déduire la probabilité d’obtenir la somme
3 en lançant les dés. On exprimera
cette probabilité en pourcentage.
Expliquer
pourquoi ce résultat est différent de celui obtenu à la question 1.
Nombre de cas possible 4 x4 = 16.
Probabilité d'obtenir 3 : 2 / 16 x100 = 12,5 %, valeur inférieure
à celle du graphe.
Le nombre de lancers est insuffisant.
Exercice 4.
Trouver le nombre
auquel je pense.
• Je pense à un nombre.
• Je lui soustrais 10.
• J’élève le tout au carré.
• Je soustrais au résultat le carré du nombre auquel j’ai pensé.
• J’obtiens alors : −340.
On note N ce nombre.
N-10 ; (N-10)2 ; (N-10)2 -N2
= -340.
N2 -20 N +100 -N2= -340 ; -20 N +100 = -340 ; 20
N = 440 ; N = 22.
|
|
|
|
Exercice 5.
On
considère que les deux hélicoptères se situent à la même altitude et
que le peloton des coureurs roule sur une route horizontale. Le schéma
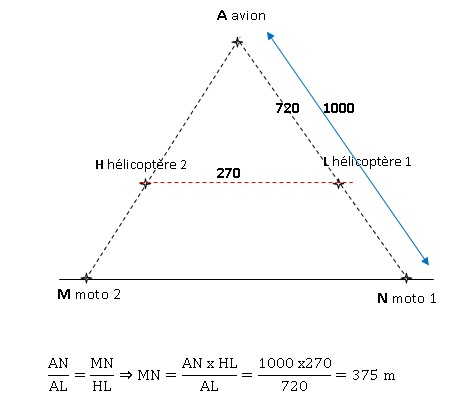
ci-dessous illustre cette situation :
L’avion relais (point A), le premier hélicoptère (point L) et la
première moto (point N) sont alignés.
De la même manière, l’avion relais (point A), le deuxième hélicoptère
(point H) et la deuxième moto (point M) sont également alignés.
On sait que : AM= AN = 1 km ; HL = 270 m et AH = AL = 720 m.
1. Relever la
phrase de l’énoncé qui permet d’affirmer que les droites (LH) et (MN)
sont parallèles.
Les deux hélicoptères se situent à la même altitude et que le peloton
des coureurs roule sur une route horizontale.
2. Calculer la
distance MN entre les deux motos.
Exercice 6.
À
l’issue de la 18e étape du tour de France cycliste 2014, les coureurs
ont parcouru 3 260,5 kilomètres depuis le départ. Le classement général
des neuf premiers coureurs est le suivant :
Classement
|
Nom
Prénom
|
Pays
d'origine
|
Temps
de course
|
1
|
Nibali
Vincenzo
|
Italie
|
80
h 45 min
|
2
|
Pinot
Thibaut
|
France
|
80
h 52 min
|
3
|
Péraud
JC
|
France
|
80
h 53 min
|
4
|
Valverde
Alejandro
|
Espagne
|
80
h 53 min
|
5
|
Bardet
Romain
|
France
|
80
h 55 min
|
6
|
Van Garderen Tejay |
Etats
Unis |
80
h 57 min
|
7
|
Mollema
Bauke
|
Pays
Bas
|
80
h 59 min
|
8
|
Ten
Dam Laurens
|
Pays
bas
|
81h00
|
9
|
Konig
Léopold
|
République
Tchèque
|
81
h00
|
1. Calculer la
différence entre le temps de course de Leopold Konig et celui de
Vincenzo Nibali.
81 h 00 - 80 h 45 min = 15 min.
2. On considère la
série statistique des temps de course.
a. Que représente
pour la série statistique la différence calculée à la question 1. ?
15 min représente l'étendue de la série.
b. Quelle est la
médiane de cette série statistique ? Vous expliquerez votre démarche.
La médiane ( 80 h 55 min ) sépare la série en deux parties ayant
le même éffectif ( 4 temps supérieurs à 80 h 55 min et 4 temps
inférieures ).
c. Quelle est la
vitesse moyenne en km.h−1 du premier français Thibaut Pinot
? Arrondir la réponse à l’unité.
80 h 52 min = 80 h +52 / 60 h =80,867 h.
Vitesse moyenne = distance ( km) / durée (h) = 3260,5 / 80,867
~40 km /h.
|
|
Exercice 7.
La
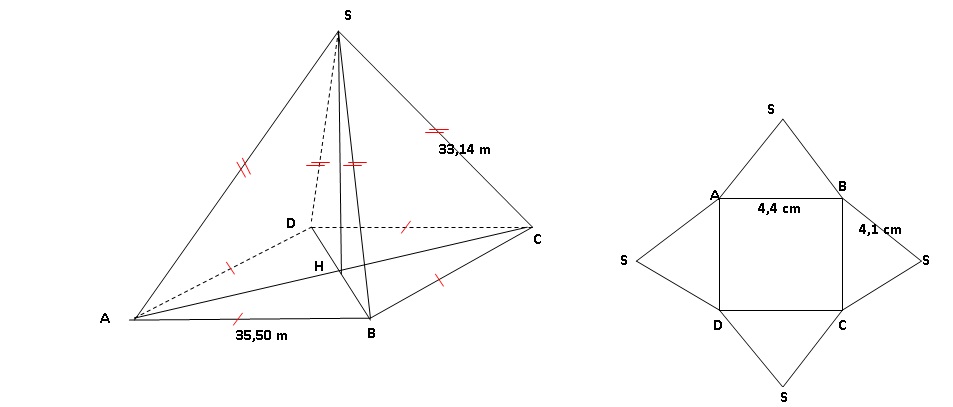
Pyramide du Louvre est une oeuvre de l’architecte Leoh Ming Pei. Il
s’agit d’une pyramide régulière dont la base est un carré de côté 35,50
mètres et dont les quatre arêtes qui partent du sommet mesurent toutes
33,14 mètres.
1. Calculer la
hauteur réelle de la Pyramide du Louvre. On arrondira le résultat au
centimètre.
DH = HC, demi-diagonale du carré ; DH2 +HC2
= DC2 ; 2DH2 = DC2 =35,502
=1260,25 ; DH2 = 630,125.
HS2= DS2 -DH2=33,142
-630,125 = 468,1346 ; HS = 21,64 m.
2. On veut tracer
le patron de cette pyramide à l’échelle 1/800.
a. Calculer les
dimensions nécessaires de ce patron en les arrondissant au millimètre.
Coté du carré : 35,50 / 800 x 1000 = 35,50 / 0,800 ~44 mm
Arête de la pyramide régulière : 33,14 / 800 x 1000~ 41 mm.
b. Construire le
patron en faisant apparaître les traits de construction. On attend une
précision de tracé au mm.
|
|