Mathématiques,
Brevet des collèges Asie 2015
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1.
Cet exercice est un QCM(questionnaire à choix multiples). Pour chaque
ligne du tableau, une seule affirmation est juste.
Sur votre copie, indiquer le numéro de la question et recopier
l’affirmation juste. On ne demande pas de justifier.
|
Questions
|
A
|
B
|
C
|
1
|
L’écriture
en notation scientifique
du nombre 587 000 000 est :
|
5,87
x10-8 Faux
|
587
x 106 Faux
|
5,87 108 Vrai.
|
2
|
Si
on développe et réduit l’expression
(x + 2)(3x − 1) on obtient :
|
3x2+5x-2
Vrai
|
3x2+6x+2
Faux
|
3x2-1
Faux
|
3
|
Dans
un parking il y a des motos et des voitures.
On compte 28 véhicules et 80
roues. Il y a donc :
x voitures et y motos.
x+y = 28 ou 2x +2y = 56
4x +2y =80
Soustraire : 2x =24 ; x = 12
|
20
voitures
Faux
|
16
voitures Faux
|
12 voitures
Vrai
|
4
|
.Le
produit de 18 facteurs
égaux à −8 s’écrit :
|
-818
Faux
|
(-8)18 Vrai
|
18
x(-8)
Faux
|
5
|
La
section d’un cylindre de
révolution de diamètre 4 cm
et de hauteur 10 cm par
un plan parallèle à son axe
peut être :
|
un rectangle
de
dimensions
3 cm et 10 cm
Vrai
|
un
rectangle
de
dimensions
5 cm et 10 cm
Faux |
un
rectangle
de
dimensions
3 cm et 8 cm
Faux |
Exercice 2.
Julien est en retard pour aller rejoindre ses amis au terrain de basket.
Il décide alors de traverser imprudemment la route du point J au point
F sans utiliser les passages piétons. Le passage piéton est supposé
perpendiculaire au trottoir.
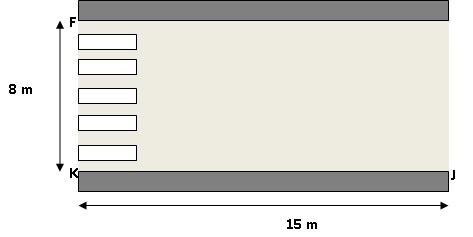
En moyenne, un
piéton met 9 secondes pour parcourir 10 mètres.
Combien de temps Julien a-t-il gagné en traversant sans utiliser le
passage piéton ?
JF2 = FK2 +JK2 = 82 +152
= 64 +225 = 289 ; JF = 17 m.
Durée du parcours JF : 17 x 9 /10 =15,3 s.
Durée du parcours JK + KF : 23 / 10 x 9 =20,7 s ; gain :
20,7-15,3 = 5,4 s.
|
| ... |
|
|
Exercice 3.
Un
bus transporte des élèves pour une compétition multisports. Il y a là
10 joueurs de ping-pong, 12 coureurs de fond et 18 gymnastes. Lors d’un
arrêt, ils sortent du bus en désordre.
1. Quelle est la
probabilité que le premier sportif à sortir du bus soit un joueur de
ping-pong ?
Nombre de cas favorables : 10 ; nombre total de joueur : 40.
Probabilité que le premier sortant joue au ping-pong : 10 / 40 = 0,25.
2. Quelle est la
probabilité que le premier sportif à sortir du bus soit un coureur ou
un gymnaste ?
Nombre
de cas favorables : 30 ; nombre total de joueur : 40.
Probabilité que le premier sortantsoit un coureur ou un gymnaste : 30 /
40 = 0,75.
3.
Après cet arrêt, ils remontent dans le bus et ils accueillent un groupe
de nageurs.
Sachant que la probabilité que ce soit un nageur qui descende du bus en
premier est de 1/5, déterminer le nombre de nageurs présents dans le
bus.
Soit x le nombre de nageurs.
Nombre total d'élèves : 40 +x ; nombre de cas favorables : x.
x / (40+x) = 1 / 5 = 0,2 ; x = 0,2 (40 +x) = 8 +0,2 x ; 0,8 x = 8 ; x =
10.
Exercice 4.
À
la fin d’une fête de village, tous les enfants présents se partagent
équitablement les 397 ballons de baudruche qui ont servi à la
décoration. Il reste alors 37 ballons.
L’année suivante, les mêmes enfants se partagent les 598 ballons
utilisés cette année là. Il en reste alors 13. Combien d’enfants, au
maximum, étaient présents ?
Soit N le nombre d'enfants : 397-37 = 360 est un multiple entier de N.
598-13 = 585 est un multiple entier de N.
360 = 23x 32 x5.
585 = 32 x 5 x 13.
PGCD de 360 et 585 : 32 x 5 =45.
|
|
|
|
Exercice 5.
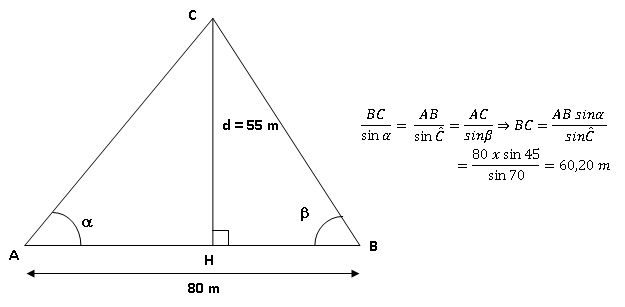
Un bateau se trouve à une distance d de la plage.Supposons dans tout le
problème que a=
45°,ß = 65° et que L =BC= 80m.
1. Conjecturons la
distance d à l’aide d’une construction
Mise au point par Thalès (600 avant JC), la méthode dite de
TRIANGULATION propose une solution pour estimer la distance d.
a. Faire un schéma à l’échelle 1/1 000 (1 cm pour 10 m).
b. Conjecturer en
mesurant sur le schéma la distance d séparant le bateau de la côte.
2. Déterminons la
distance d par le calcul.
a. Expliquer
pourquoi la mesure de l’angle ACB est de 70°.
La somme des angles d'un triangle est égale à 180 ° : 180-45-65 = 70°.
b. Dans tout
triangle ABC, on a la relation ci-dessus appelée « loi des sinus » :
En utilisant cette formule, calculer la longueur BC. Arrondir au cm
près.
c. En déduire la
longueur CH arrondie au cm près.
sin ß =CH / BC ; CH
= BC sin ß = 60,2 x sin 65 = 54,56 m.
Exercice 6.
Soient les fonctions f , g et h définies par :
f (x) = 6x ; g (x)= 3x2 −9x −7 et h(x) = 5x −7.
À l’aide d’un tableur, Pauline a construit un tableau de valeurs de ces
fonctions.
Elle a étiré vers la droite les formules qu’elle avait saisies dans les
cellules B2, B3 et B4.
B3
|
=3*B1*B1-9*B1-7
|
|
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
1
|
x
|
-3
|
-2
|
-1
|
0
|
1
|
2
|
3
|
2
|
f(x)=6x
|
-18
|
-12
|
-6
|
0
|
6
|
12
|
18
|
3
|
g(x)
=3x2-9x-7
|
47
|
23
|
5
|
-7
|
-13
|
-13
|
-7
|
4
|
h(x)=5x-7
|
-22
|
-17
|
-12
|
-7
|
-2
|
3
|
8
|
1. Utiliser le
tableur pour déterminer la valeur de h(−2).
h(-2) = -17.
2. Écrire les
calculs montrant que : g (−3) = 47.
3*(-3)*(-3) -9*(-3)-7=3*9+27-7=47
3. Faire une phrase
avec lemot « antécédent » ou le mot « image » pour traduire l’égalité g
(−3) = 47.
L'image de (-3) par la fonction g est 47 ; l'antécédent de 47 par la
fonction g est (-3).
4. Quelle formule
Pauline a-t-elle saisie dans la cellule B4 ?
= 5 *B1 -7
5. a. Déduire du
tableau ci-dessus une solution de l’équation : 3x2−9x −7 =
5x −7.
x=0.
b. Cette équation
a-t-elle une autre solution que celle trouvée grâce au tableur ?
Justifier la réponse.
3x2−9x −7 -( 5x −7)=0 ; 3x2−9x-5x=0 ; x(3x-14)=0
; solution x = 0 et x = 14 / 3.
|
|
Exercice 7.
Un aquarium a la forme d’une sphère de 10
cm de rayon, coupée en sa partie haute : c’est une « calotte sphérique
».
La hauteur totale de l’aquarium est 18 cm.
1. Le volume d’une
calotte sphérique est donné par la formule : V = p / 3 h2
(3r-h).
où r est le rayon de la sphère et h est la hauteur de la calotte
sphérique.
a. Prouver que la
valeur exacte du volume en cm3 de l’aquarium est 1296 p.
V = p / 3 x 182(3x10-18)=1296
p.
b.
Donner la valeur approchée du volume de l’aquariumau litre près.
1296 x3,14 ~ 4071 cm3 ~ 4 L.
2. On remplit cet
aquarium à ras bord, puis on verse la totalité de son contenu dans un
autre aquarium parallélépipédique. La base du nouvel aquarium est un
rectangle de 15 cm par 20 cm.
Déterminer la hauteur atteinte par l’eau (on arrondira au cm).
15 x 20 x h = 4071 ; h = 4071 /(15 x 20) = 13,57 ~14 cm.
|
|