Mathématiques,
Brevet des collèges Polynésie 2015
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1.
Djamel
et Sarah ont un jeu de société : pour y jouer, il faut tirer au hasard
des jetons dans un sac. Tous les jetons ont la même probabilité d’être
tirés. Sur chaque jeton un nombre entier est inscrit. Djamel et Sarah
ont commencé une partie. Il reste dans le sac les huit jetons suivants
::
5 14 26 18 5 9 18 20
1. C’est à Sarah de
jouer.
a. Quelle est la
probabilité qu’elle tire un jeton « 18 » ?
2 cas favorables sur 8 cas possibles : 2 / 8 = 0,25.
b. Quelle est la
probabilité qu’elle tire un jeton multiple de 5 ?
3 cas favorables ( 5 ; 5 ; 20) : 3 /8 = 0,375.
2. Finalement,
Sarah a tiré le jeton « 26 » qu’elle garde. C’est au tour de Djamel de
jouer.
La probabilité qu’il tire un jeton multiple de 5 est-elle la même que
celle trouvée à la question 1. b. ?
Non, 3 cas sont favorables parmi 7 possibilités : 3 / 7.
Exercice 2.
1.
Le graphique ci-dessous donne le niveau de bruit (en décibels) d’une
tondeuse à gazon en marche, en fonction de la distance (en mètres)
entre la tondeuse et l’endroit où s’effectue la mesure.
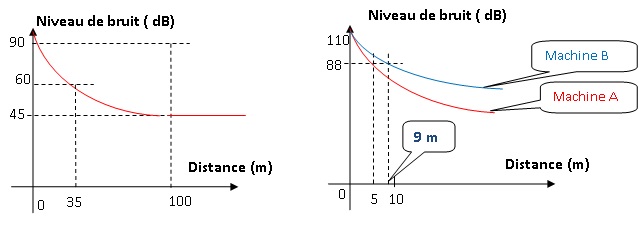
a. Quel est le
niveau de bruit à une distance de 100 mètres de la tondeuse ? 45 dB.
b. À quelle
distance de la tondeuse se trouve-t-on quand le niveau de bruit est
égal à 60 décibels ?
35 m.
2. Voici les
graphiques obtenus pour deux machines très bruyantes d’une usine.
Dans l’usine, le port d’un casque antibruit est obligatoire à partir
d’un même niveau de bruit.
Pour la machine A, il est obligatoire quand on se trouve à moins de 5
mètres de la machine. En utilisant ces graphiques, déterminer cette
distance pour la machine B. ( 9 m).
|
| ... |
|
|
Exercice 3.
On considère la figure ci-dessous dessinée à main
levée. L’unité utilisée est le centimètre.
Les points I, H et K sont alignés.
1. Construire la
figure en vraie grandeur.
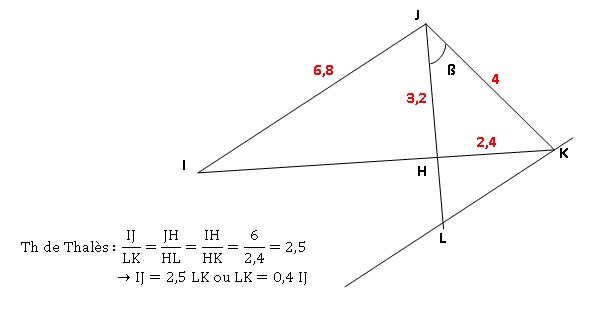
2. Démontrer que
les droites (IK) et (JH) sont perpendiculaires.
JK2 = 42 = 16 cm2.
JH2 + HK2 = 3,22 +2,42
=10,24+5,76 =16.
JK2
=JH2 + HK2 :
d'après la réciproque du théorème de Pythagore, le triangle JHK
est rectangle en H.
3.
Démontrer que IH = 6 cm.
IH2 = IJ2 -JH2 = 6,82-3,22=46,24-10,24
=36 ; IH = 6 cm.
4. Calculer la
mesure de l’angle ß, arrondie au degré.
tan ß = HK / JH = 2,4 / 3,2 = 0,75 ; ß ~37°.
5. La parallèle à
(IJ) passant par K coupe (JH) en L. Compléter la figure.
6. Expliquer
pourquoi LK = 0,4× IJ.
(IJ) et (LK) sont parallèles et (IK) et JL) sont sécantes. Utiliser le
théorème de Thalès.
Exercice 4.
1. Quel est le
pourcentage de remise ?
Ancien prix 80 €
Nouveau prix 60 €.
(80-60) / 80 x 100 = 25 %.
2. 2 048 est une
puissance de 2. Laquelle ?
25 = 32 ; 210 =32 x32 = 1024 ; 211 =
2048.
3. En développant
l’expression (2x−1)2 , Jules a obtenu 4x2 −4x−1.
A-t-il raison ?
Non, il faut écrire : 4x2 -4x +1.
|
|
|
|
Exercice 5.
Les « 24 heures duMans »est le nomd’une course automobile.
La longueur d’un tour est de 13,629 km
5 405,470 est le nombre de kilomètres parcourus par l’Audi R15+ à
l’issue de la course.
1. Déterminer le
nombre de tours complets que la voiture Audi R15+ a effectués lors de
cette course.
5405,470 / 13,629~396,6 tours.
2. Calculer la
vitesse moyenne en km/h de cette voiture. Arrondir à l’unité.
5405,470 /24 =225,23 ~225 km /h.
3. On relève la
vitesse de deux voitures au même moment :
• Vitesse de la voiture n° 37 : 205 mph.
• Vitesse de la voiture n° 38 : 310 km/h.
Quelle est la voiture la plus rapide ?
L’unité de mesure utilisée par les anglo-saxons est le mile par heure
(mile per hour) noté mph.
1mile ≈ 1 609 mètres.
205 x 1,609 =329,8 km /h. La voiture n°37 est la plus rapide.
Exercice 6.
Voici un programme de calcul.
• Choisir un nombre
• Ajouter 1
• Calculer le carré de cette somme
• Soustraire 9 au résultat.
1. Vérifier qu’en
choisissant 7 comme nombre de départ, le résultat obtenu avec ce
programme est 55.
(7+1)2 -9 = 64-9=55.
2. Lorsque le
nombre choisi est −6, quel résultat obtient-on ?
(-6 +1)2-9 = 25-9=16.
3. Jim utilise un
tableur pour essayer le programme de calcul avec plusieurs nombres. Il
a fait apparaître les résultats obtenus à chaque étape. Il obtient la
feuille de calcul ci-dessous :
|
A
|
B
|
C
|
D
|
1
|
Nombre
de départ
|
Résultat
1ère étape
|
Résultat
2ème étape
|
Résultat
final
|
2
|
0
|
1
|
1
|
-8
|
3
|
0,8
|
1,8
|
3,24
|
-5,76
|
4
|
1,2
|
2,2
|
4,84
|
-4,16
|
5
|
2
|
3
|
9
|
0
|
La colonne B est obtenue à partir d’une formule écrite en B2, puis
recopiée vers le bas.
Quelle formule Jim a-t-il saisie dans la cellule B2 ?
=A2+1
4. Le programme
donne 0 pour deux nombres. Déterminer ces deux nombres.
(x+1)2-32 = 0.
(x+1+3) ( x+1-3) =0.
(x+4) (x-2)=0.
Solutions x = 2 et x = -4.
|
|
Exercice 7.
Voici les caractéristiques d’une piscine qui doit être rénovée :
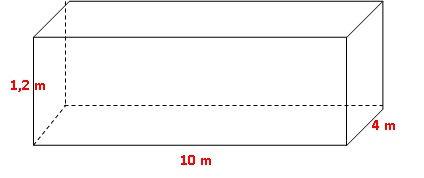
Débit de la pompe de vidange : 14 m3/h.
informations sur la peinture résine utilisée pour la rénovation
seau de 3 litres ; un litre recouvre une surface de 6 m2
; 2 couches nécessaires ; prix du seau : 69,99 €.
1. Le propriétaire
commence par vider la piscine avec la pompe de vidange.
Cette piscine est remplie à ras bord. Sera-t-elle vide en moins de 4
heures ?
Volume de la piscine : 1,2 x 10 x 4 = 48 m3.
Durée de la vidange : 48 / 14 =3,4 heures, valeur inférieure à 4 heures.
2. Il repeint
ensuite toute la surface intérieure de cette piscine avec de la
peinture résine. Quel est le coût de la rénovation ?
Aire du fond = 10 x4 = 40 m2.
Aire latérale : (10 +4 +10 +4 ) x1,2 =33,6 m2.
Aire totale : 73,6 m2.
Nombre de seau pour deux couches de peintures : 2 x 73,6 /18=8,17
, donc 9 seaux.
Coût : 9 x 69,99 = 629,91 €.
|
|