Mathématiques,
Brevet des collèges Asie 2016
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
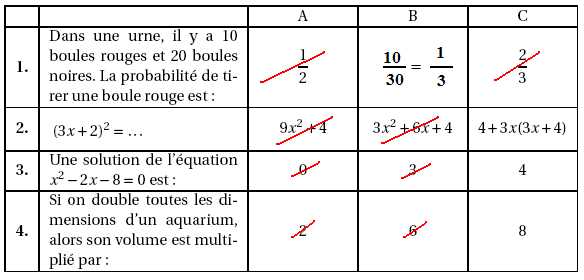
Exercice 1.
Cet
exercice est un questionnaire à choix multiple (QCM). Pour chaque ligne
du tableau, trois réponses sont proposées,mais une seule est exacte.
Toute réponse exacte vaut 1 point.
Toute réponse inexacte ou toute absence de réponse n’enlève pas de
point.
Indiquez sur votre copie le numéro de la question et, sans justifier,
recopier la réponse exacte (A ou B ou C).
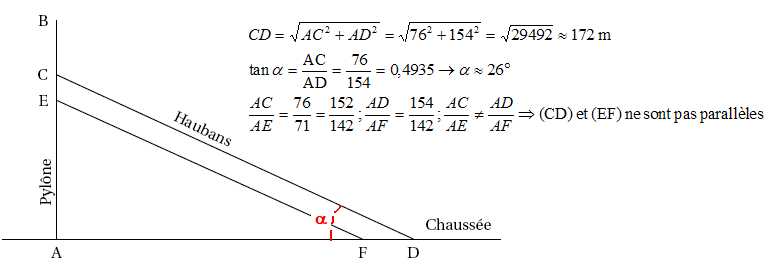
Exercice 2.
Le viaduc de
Millau est un pont franchissant la vallée du Tarn, dans le département
de l’Aveyron, en France. Il est constitué de 7 pylônes verticaux
équipés chacun de 22 câbles appelés haubans.
Le schéma ci-dessous, qui n’est pas à l’échelle, représente un pylône
et deux de ses haubans.
On dispose des
informations suivantes :
AB = 89 m ; AC = 76 m ; AD = 154 m ; FD = 12 m et EC = 5m.
1. Calculer la
longueur du hauban [CD]. Arrondir au mètre près.
2. Calculer la
mesure de l’angle �CDA formé par le hauban [CD] et la chaussée.
Arrondir au degré près.
3. Les haubans [CD]
et [EF] sont-ils parallèles ?
|
| ... |
|
|
Exercice 3.
Une entreprise de fabrication de bonbons souhaite
vérifier la
qualité de sa nouvelle machine de conditionnement. Cette machine est
configurée pour emballer environ 60 bonbons par paquet. Pour vérifier
sa bonne configuration, on a étudié 500 paquets à la sortie de cette
machine.
| Nombre
de bonbons xi |
56 |
57 |
58 |
59 |
60 |
61 |
62 |
63 |
64 |
Total |
| Effectifs
ni |
4 |
36 |
53 |
79 |
145 |
82 |
56 |
38 |
7 |
500 |
| ni(xi-xmoy)2 |
64 |
324 |
212 |
79 |
0 |
82 |
224 |
342 |
112 |
1439 |
Pour être validée par l’entreprise, la
machine doit respecter trois critères de qualité :
• Le nombre moyen de bonbons dans un paquet doit être compris entre
59,9 et 60,1.
• L’étendue de la série doit être inférieure ou égale à 10.
•
L’écart interquartile (c’est-à-dire la différence entre le troisième
quartile et le premier quartile) doit être inférieur ou égal à 3. La
nouvelle machine respecte-t-elle les critères de qualité ?
Moyenne : xmoy=(56 +57 +58 +59 +60 +61 +62 +63 +64) / 9 =60.
Etendue de la série 64-56 = 8.
Variance : V = 1439 /500 =2,878 ; écart type : 2,878½ ~1,7.
Les trois critères de qualité sont respectés.
Exercice 4.
Adèle
et Mathéo souhaitent participer au marathon de Paris. Après s’être
entraînés pendant des mois, ils souhaitent évaluer leur état de forme
avant de s’engager. Pour cela, ils ont réalisé un test dit « de Cooper
» : l’objectif est de courir, sur une piste d’athlétisme, la plus
grande distance possible en 12 minutes. La distance parcourue détermine
la forme physique de la personne.
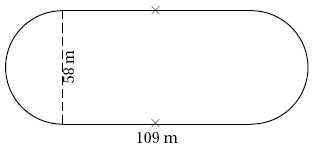
1. Vérifier que la
longueur de la piste est d’environ 400 mètres.
109 +109 +3,14 x 58 ~400 m.
2.
Adèle et Mathéo ont décidé de participer au marathon uniquement si leur
indice de forme est au moins au niveau «moyen ». Déterminer si
Adèle et Mathéo participeront à la course.
Adèle a réalisé 6 tours de piste et 150 mètres soit une distance
parcourue de 6 x400 +150 = 2550 m.
Cette distance étant supérieure à 2500 m, l'indice de forme d'Adèle est
"très bon".
Mathéo a réalisé le test avec une vitesse moyenne de 13,5 km/h.
12 min = 12 / 60 = 0,2 heure ; distance parcourue : 13,5 x0,2 = 2,7 km
= 2700 m.
Cette
distance étant comprise entre 2401 et 2800 m, l'indice de forme de
Mathéo est " bon".
Ils participeront donc à la course.
|
|
|
|
Exercice 5.
On considère les fonctions f et g définies par : f (x) = 2x +1 et g (x)
= x2 +4x −5.
Léa
souhaite étudier les fonctions f et g à l’aide d’un tableur. Elle a
donc rempli les formules qu’elle a ensuite étirées pour obtenir le
calcul de toutes les valeurs. Voici une capture d’écran de son travail :
| B3 |
=B1*B1+4*B1-5 |
|
A |
B |
C |
D |
E |
F |
G |
H |
| 1 |
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
| 2 |
f(x) |
-5 |
-3 |
-1 |
1 |
3 |
5 |
7 |
| 3 |
g(x) |
-8 |
-9 |
-8 |
-5 |
0 |
7 |
16 |
| 4 |
|
|
|
|
|
|
|
|
1. Quelle est
l’image de 3 par la fonction f ? 7.
2. Calculer le
nombre qui doit apparaître dans la cellule C3.
g(-2)=(-2)2 +4*(-2) -5 = 4-8-5= -9.
3. Quelle formule
Léa a-t-elle saisie dans la cellule B2 ?
=2*B1+1.
4. À l’aide de la
copie d’écran et sans justifier, donner une solution de l’inéquation 2x
+1 < x2+4x −5.
x = 2 ; x = 3.
5. Déterminer un
antécédent de 1 par la fonction f . 0.
Exercice 6.
Dans chaque cas, dire si l’affirmation est vraie ou fausse. Justifier
votre réponse.
1. Affirmation 1 :
Deux nombres impairs sont toujours premiers entre eux. Faux.
5 et 15 sont impairs mais ils ne sont pas premiers entre eux.
2. Affirmation 2 :
Pour tout nombre entier positif a et b, 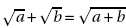 Faux. Faux.
3. Affirmation 3 :
Si on augmente le prix d’un article de 20% puis de 30% alors, au total,
le prix a augmenté de 56%. Vrai.
Facteur multiplicatif : (1+0,2) x(1+0,3) = 1,2 x 1,3 = 1,56.
|
|
Exercice 7.
Romane
souhaite préparer un cocktail pour son anniversaire.

Le récipient choisi par Romane est-il assez grand pour préparer le
cocktail pour 20 personnes ?
Volume du cocktail pour 6 personnes : 60 +30 +12 +12 = 114 cL soit 114
/ 6 = 19 cL par personne.
Volume du cocktail pour 20 personnes : 19 x 20 = 380 cL ou 3,8 L.
Volume du récipient : 2 /3 p
R3 = 2 / 3 x3,14 x133 =4601 cm3 ou 4,6
L.
Le récipient est assez grand.
|
|