Math�matiques,
Brevet des coll�ges M�tropole septembre 2016
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicit�s adapt�es � vos centres
d’int�r�ts.
|
|
|
|
|
|
Exercice 1.
Le graphique ci-dessous repr�sente la hauteur d’eau dans le port de
Brest, le 26 octobre 2015
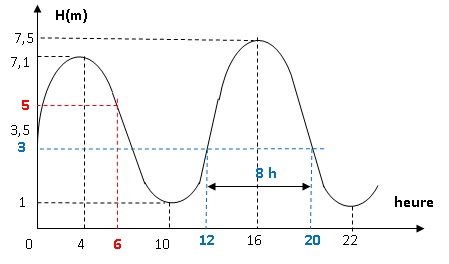
1. En utilisant ce
graphique r�pondre aux questions suivantes.
a. Le 26 octobre
2015 quelle �tait environ la hauteur d’eau � 6 heures dans
le port de Brest.
b. Le 26 octobre
2015 entre 10 heures et 22 heures, pendant combien de
temps environ la hauteur d’eau a-t-elle �t� sup�rieure � 3 m�tres ?
2. En France,
l’ampleur de la mar�e est indiqu�e par un nombre entier appel� �
coefficient de mar�e �. Au port Brest, il se calcule gr�ce � la formule
:
C =(H −N0) / U �100
en donnant un r�sultat arrondi � l’entier le plus proche avec :
• C : coefficient de mar�e
• H : hauteur d’eau maximale en m�tres pendant la mar�e
• N0 = 4,2 m(niveau moyen � Brest)
• U = 3,1 m(unit� de hauteur � Brest).
C = (7,5-4,2) /3,1 x 100 = 106.
Exercice 2.
Sur la figure le point J appartient
au segment [IM] et le point K appartient au segment [IL].
Sur la figure, les longueur sont donn�es en m�tres.
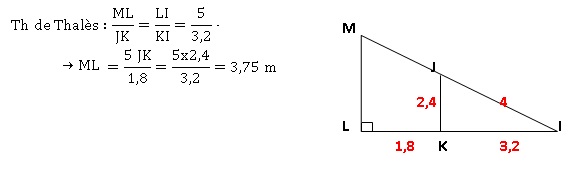
1. Montrer que IKJ
est un triangle rectangle.
IJ2 = 16 ; JK2 + KI2 = 2,42
+3,22 = 16.
IJ2 =JK2
+ KI2 : d'apr�s la r�ciproque du th�or�me de
Pythagore, le triangle IJK est rectangle en K.
2. Montrer que LM est �gal � 3,75 m.
(ML) et (JK) sont parall�les, �tant toutes
deux perpendiculaires � (IL).
Th�or�me de Thal�s ( IM et IL sont deux s�cantes).
3. Calculer la longueur KM au
centim�tre pr�s.
KM2 = ML2 + KL2 = 3,752 +1,82
= 17,30 ; KM = 4,16 m.
|
|
|
Exercice 3.
La feuille de calcul suivante donne
la production mondiale de vanille en 2013.
|
A
|
B
|
1
|
Pays
|
Production
( milliers de tonnes)
|
2
|
Chine
|
335
|
3
|
Comores
|
35
|
4
|
France
|
79
|
5
|
Indon�sie
|
3200
|
6
|
Kenya
|
15
|
7
|
Madagascar
|
3100
|
8
|
Malawi
|
22
|
9
|
Mexique
|
463
|
10
|
Ouganda
|
161
|
11
|
Papouasie |
433 |
12
|
Tonga
|
198
|
13
|
Turquie
|
290
|
14
|
Zinbabwe
|
11
|
15
|
Total
|
8342
|
1. Quelle formule
de tableur a �t� saisie dans la cellule B15 ?
=SOMME(B2 : B14)
2. � eux deux,
l’Indon�sie et Madagascar produisent-ils plus des trois quarts de la
production
mondiale de vanille ?
3200 +3100 = 6300 ; 6300 / 8342 x100 =75,5 % (r�ponse oui).
3. On s’int�resse
aux cinq pays qui ont produit le moins de vanille en 2013.
Quel pourcentage de la production mondiale repr�sente la production de
vanille de ces
cinq pays ? Arrondir le r�sultat � l’unit�.
35+79+15+22+11=162 ; 162 / 8342 x100 ~2 %.
Exercice 4.
Cet exercice est un
questionnaire � choix multiple. Aucune justification n’est attendue.
Pour chacune des questions, une seule r�ponse est exacte.
Recopier sur la copie le num�ro de la question et la r�ponse exacte.
Toute r�ponse exacte vaut 1.5 point. Toute r�ponse inexacte ou toute
absence de
r�ponse n’enl�ve pas de point.
Question 1
Le nombre 2 est solution de l’in�quation :
a. x < 2 (
faux); b. −4x −3 >
−10 ( faux) ; c. 5x -4<=7 (
vrai) ; d. 8−3x >=3 (faux).
Question 2.
La fonction f qui � tout nombre x associe le nombre 2x −8 est
repr�sent�e par le graphe :
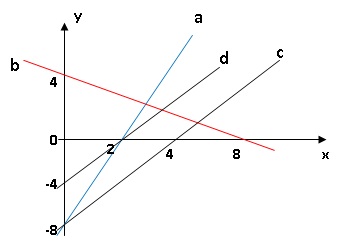
Graphe c car f(0) = -8 et
f(4) = 0.
Question 3.
Un coureur qui parcourt
100 m�tres en 10 secondes a une vitesse �gale :
a. 6 km/min ; b. 36 km/h (vrai); c. 3 600 m/h ; d. 10 km/h.
100 /10 =10 m /s ou 10 x3,6 = 36 km/h.
|
|
|
|
Exercice 5.
Sur un blog de couture, Archibald a trouv� une fiche technique pour
tracer un pentagramme (�toile � cinq branches).
1. Tracer un cercle de centre O, puis tracer deux diam�tres
perpendiculaires [AB] et [CD].
2. Placer le milieu du segment [OC]. Le nommer J.
3. Placer la pointe du compas sur J, placer le crayon sur C et tourner.
4. Repr�senter la demi-droite [JA]. Elle coupe ce cercle en M.
5. Placer la pointe du compas sur A, placer le crayon sur M et tourner.
6. Le cercle obtenu coupe le cercle de centre O et de rayon [OC] en E
et F.
7. � partir du point F, reporter trois fois la longueur EF sur le
cercle pour obtenir dans cet ordre les points G, H et I.
8. Tracer les segments [EG], [GI], [IF], [FH] et [HE].
1. Compl�ter et
terminer la construction de l’�toile � cinq branches d�but�e par
Archibald. On fera appara�tre les points B, D, J,M, E, F,
G, H et I.
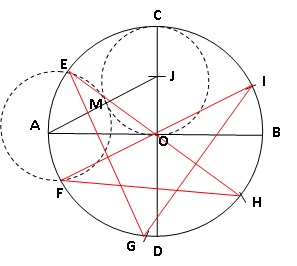
2. R��crire la
troisi�me consigne sur la copie en utilisant le vocabulaire
math�matique adapt�.
Tracer le cercle de centre J et de rayon �OC.
3. En utilisant
cette fiche technique, Ana�s a obtenu la construction ci-dessus. Elle
mesure les angles EGI et EHI et constate qu’ils sont �gaux. Est-ce le
cas pour tous les pentagrammes construits avec cette m�thode ?
Oui, les angles inscrits EGI et EHI interceptent le m�me arc de cercle.
Ils ont donc la m�me mesure.
Exercice 6.
M�lanie construit une v�randa contre l’un des murs de sa maison.
Pour couvrir le toit de la v�randa, elle se rend chez un grossiste en
mat�riaux qui lui fournit des renseignements concernant deux mod�les de
tuiles.
Mod�le
|
Tuile
romane
|
Tuile
r�gence
|
Coloris
|
littoral
|
brun
vieilli
|
Quantit�
au m2
|
13
|
19
|
Poids
au m2
|
44
|
44
|
Pente
minimale du toit
|
15
|
18
|
Prix
unitaire
|
1,79
€
|
1,2
€
|
Prix
au m2
|
23,27
€
|
.....
|
1. Calculer le prix
au m2 des � tuiles r�gence �.
1,2 x19 =22,80 €.
2. La pente du toit
de la v�randa, c’est-�-dire l’angle DEC, permet-elle la pose de chaque
mod�le ?
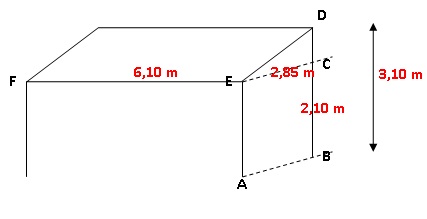
tan DEC = DC / EC = 1,00 / 2,85 = 0,351 ; l'angle DEC mesure
19,3�, valeur sup�rieure � 18�. La pente du toit permet la pose
de chaque mod�le.
3. M�lanie d�cide
finalement de couvrir le toit de sa v�randa avec des tuiles romanes.
Ces tuiles sont vendues � l’unit�.
Pour d�terminer le nombre de tuiles � commander, le vendeur lui
explique :
� Il faut d’abord calculer la surface � recouvrir. Il faut augmenter
ensuite cette surface de 5%. �
En tenant compte de ce conseil, combien de tuiles doit-elle pr�voir
d’acheter ?
ED2 = DC2 +EC2 =12 +2,852
= 9,12 ; ED = 3,02 m.
Surface du toit S = 6,10 x 3,02 = 18,4 m2.
Nombre de tuils : 18,42 x 1,05 x 13 ~252.
|
|
Exercice 7.
Une pizzeria fabrique des pizzas rondes de 34 cm de diam�tre et des
pizzas carr�es de 34 cm de c�t�.
Toutes les pizzas ont lam�me �paisseur et sont livr�es dans des bo�tes
identiques.
Les pizzas carr�es co�tent 1 € de plus que les pizzas rondes.
1. Pierre ach�te
deux pizzas : une ronde et une carr�e. Il paye 14,20 €. Quel est le
prix de chaque pizza ?
x : prix d'une pizza ronde ; x +x+1 = 14,20 ; 2x = 13,20 ; x = 13,20 /
2 = 6,60 €.
2. Les pizzas
rondes sont d�coup�es en huit parts de m�me taille et les pizzas
carr�es en neuf parts de m�me taille.
Dans quelle pizza trouve-t-on les parts les plus grandes ?
Aire d'une pizza ronde : pr2
=3,14 x172~ 908 cm2 ; aire d'une part : 908
/ 8 ~113 cm2.
Aire
d'une pizza carr�e : 342 = 1156 cm2 ; aire d'une
part : 1156 / 9 ~128 cm2, part la plus grande.
|
|
