Mathématiques,
Brevet des collèges Nlle Calédonie 2016
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1. QCM
1. Si une voiture
roule à une allure régulière de 60 km/h, quelle distance va-t-elle
parcourir en 1 h 10
min ?
1 h 10 min = 1,167 h ; 60 x1,167 ~70 km ( proposition B).
2. Dans la salle 1
du cinéma, il y a 200 personnes dont 40% sont des femmes. Dans la salle
2, sur les 160 personnes, 50% sont des femmes. Quelle affirmation est
vraie ?
A. Il y a plus de femmes dans la salle 1. Faux.
B. Il y a plus de femmes dans la salle 2. faux.
C. Il y a autant de femmes dans les deux salles. Vrai.
Salle 1 : 200 xx0,4 = 80 frmmrd ; salle 2 : 160 x0,5 = 80 femmes.
3. Quelle est
l’aire d’un carré dont les côtés mesurent 10 cm ?
10 cm2 faux ; 1 dm2 vrai ; 1 m2 faux.
4. 11 +22
+33 =1 +4 +9 = 14 ( proposition B).
5. Quelle est la
solution de l’équation 2x +4 = 5x −2 ?
4+2 = 5x-2x ; 6 =3x ; x = 2 (proposition C).
Exercice 2.
Dans
un jeu vidéo, pour gagner des points d’expérience et faire évoluer son
personnage, il faut participer à des combats. Chaque victoire rapporte
un nombre de points fixe. Il en est de même pour chaque défaite.
Gabriel a déjà accumulé 1 350 points avec 21 victoires et 9 défaites.
Son frère Nathaniel a obtenu 12 victoires pour 18 défaites et a
totalisé 900 points.
Combien de points gagne-t-on à ce jeu en cas de victoire ? En cas de
défaite ? On écrira les calculs qui permettent de justifier les
réponses.
x : nombre de points pour une victoire ; y : nombre de points pour une
défaite.
21x +9y = 1350 ; 12x +18 y = 900.
42x +18y = 2700 ; 12x +18 y = 900.
Soustraire : 30x = 1800 ; x = 1800 / 30 = 60 ;
9y = 1350 -21 *60 = 90 ; y= 90 / 9 = 10.
60 points pour une victoire et 10 points pour une défaite.
|
| ... |
|
|
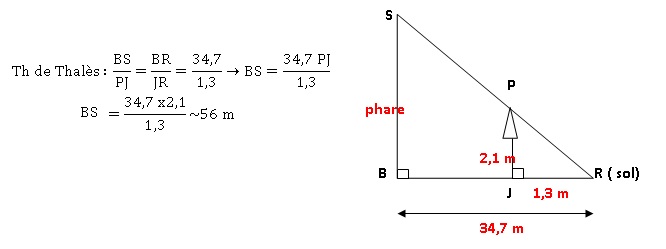
Exercice 3.
Pendant les vacances, Robin est allé
visiter le phare Amédée. Lors d’une sieste
sur la plage il a remarqué que le sommet d’un parasol était en parfait
alignement avec le sommet du phare.
Robin a donc pris quelques mesures et a décidé de faire un schéma de la
situation dans le sable pour trouver une estimation de la hauteur du
phare.
Les points B, J et R sont alignés.
(SB) et (BR) sont perpendiculaires.
(PJ) et (BR) sont perpendiculaires.
Quelle hauteur, arrondie aumètre, va-t-il trouver à l’aide de son plan
? Justifier la réponse.
Exercice 4.
Thomas et Hugo
décident d’aller marcher ensemble. Thomas fait des pas de 0,7 mètre
à un rythme de 5 pas toutes les 3 secondes. Hugo, lui, fait des pas de
0,6 mètre au rythme de 7 pas en 4 secondes.
Lequel des deux avance le plus vite ? Expliquer la réponse.
Thomas : 0,7 x5 / 3 = 1,17 m /s.
Hugo : 0,6 x7 / 4 = 1,05 m/s.
Thomas avance le plus vite.
|
|
|
|
Exercice 5.
Voici deux programmes de calcul :
Programme A
Choisir un nombre de départ
Multiplier ce nombre par - 3
Soustraire 12 au résultat
Écrire le résultat.
Programme B
Choisir un nombre de départ
Multiplier ce nombre par 2
Ajouter 5 au résultat
Multiplier le tout par 3
Écrire le résultat.
1. On choisit −8
comme nombre de départ.
a. Prouver par le
calcul que le résultat obtenu avec le programme A est 12.
-8 x(-3)-12 = 24-12 = 12.
b. Calculer le
résultat final avec le programme B.
(-8 x2 +5) x3 = -33.
2. Sandro
affirme : « Si on choisit le même nombre de départ pour les deux
programmes, le résultat du programme A est toujours supérieur à celui
du programme B. » Prouver qu’il se trompe.
On choisit le nombre n :
A : -3n -12 ; B : ( 2n+5) x3= 6 n +15.
Comparons -3n-12 et 6n +15.
Egalité : -3n-12 = 6n +15 ; 9n = -27 ; n = -3.
Supérieur : -3n-12 > 6n +15 ; -27 > 9n ; n
< -3.
si n < -3, le résultat du programme A
est supérieur à celui du programme B.
3. Anne affirme :
«Avec le programme B j’ai trouvé un résultat égal à mon nombre de
départ ». Quel était son nombre de départ ?
(2n+5) x3 = n ; 6 n+15 = n ; 5n =
-15 ; n = -3.
Exercice 6.
Pour
son mariage, un couple souhaite décorer la salle avec des chandeliers
ornés de bougies dorées et de bougies argentées. Les futurs mariés ont
commandé sur un site internet une fin de stock et reçoivent donc 180
bougies dorées et 108 bougies argentées.
Ils veulent préparer le plus de chandeliers identiques possible sans
gaspillage. C’est à dire que :
• Le nombre de bougies dorées est le même dans tous les chandeliers.
• Le nombre de bougies argentées est aussi le même dans tous les
chandeliers.
• Toutes les bougies doivent être utilisées.
1. Combien de
chandeliers doivent-ils acheter ? Justifier la réponse.
180 = 22 x 32 x 5 ; 108 = 22 x33
;
le PGCD de 180 et 108 est égal à 22 x 32 = 36.
2. Combien de
bougies de chaque couleur y aura-t-il sur chaque chandelier ?
Chaque chandelier compte 5 bougies dorées et 3 bougies argentées.
|
|
Exercice 7.
Trois
jeunes amis décident de travailler le soir après les cours pour gagner
un peu d’argent. Comme ils ont le permis de conduire, ils s’orientent
vers la livraison de
pizzas. Ils ont réussi à trouver un emploi dans trois pizzerias
différentes.
• David va recevoir un salaire fixe de 70 000 F par mois.
• Guillaume aura un salaire mensuel composé d’une partie fixe de 50 000
F à laquelle s’ajoutent 100 F par livraison effectuée.
• Angelo sera payé chaque mois 200 F par livraison.
1. Si durant un
mois les pizzerias ne reçoivent que très peu de commandes, qui devrait
gagner le plus d’argent ?
David, car il reçoit un salaire fixe, suprérieur à la part fixe des
deux autres..
2. a. Compléter le tableau.
Nombre
de livraisons pr mois
|
50
|
200
|
300
|
600
|
Salaire
de David en F
|
70
000
|
70
000
|
70
000
|
70
000
|
Salaire
de Guillaume en F
|
55
000
|
50
000 +200 x100
=70 000
|
50
000 +300 x100
=80 000 |
50
000 +600 x100
=110 000 |
Salaire
d'Angelo en F
|
50
x200
=10 000
|
200
x 200
=40 000
|
300
x 200
=60 000
|
600
x200
=120 000
|
b.
Durant un mois, combien de livraisons Guillaume doit-il effectuer pour
avoir le même salaire que celui de David ? 200.
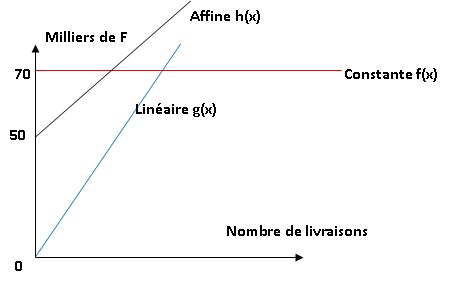
3. Dans cette
question, x désigne le nombre de livraisons effectuées durant un mois.
f , g et h sont trois fonctions définies par :
f (x) = 70000 ; g (x) = 200x ; h(x) = 100x +50000.
a. Associer
chacune de ces fonctions à l’un des trois salaires.
f(x) : David ; g(x) : Angelo ; h(x) :: Guillaume.
b. Dans le repère
suivant, écrire le nom de la fonction correspondant à chaque droite.
Exercice 8 : À
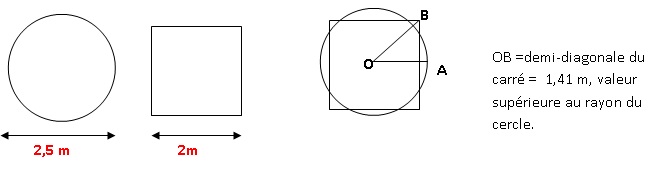
table.
Alexis a une table carrée de 2 mètres de côté. Au magasin, la seule
nappe qui lui plaît est une nappe ronde de 2,5 mètres de diamètre.
Cette nappe sera-t-elle assez grande pour recouvrir entièrement la
table (évidemment, Alexis ne découpera pas la nappe) ? Justifier la
réponse.
Non :
Exercice 9.
On souhaite organiser une chasse au trésor dans toute la
Nouvelle-Calédonie. Des balises seront cachées dans chacune des trois
Provinces de Nouvelle-Calédonie.
Certaines d’entre-elles contiendront une clé.
Voici leur répartition :
- en Province Sud sont situées 7 balises, dont 4 avec une clé,
- en Province Nord sont situées 5 balises, dont 3 avec une clé,
-en Province des Iles sont situées 3 balises, dont 2 avec une clé.
1. L’équipe des
Notous a découvert une balise en Province Nord. Quelle est la
probabilité qu’une clé se trouve à l’intérieur ?
3 cas favorables sur 5 possibilités : probabilité de trouver une clé :
3/5 = 0,6.
2. L’équipe des
Notous a bien trouvé une clé dans cette première balise. Ils découvrent
une seconde balise en Province Nord. Quelle est la probabilité qu’elle
contienne une clé ?
2 cas favorables sur 4 possibilités :
probabilité de trouver une clé : 2 / 4 = 0,5.
3.
L’équipe des Cagous a découvert deux balises dans la Province des Îles.
Quelle est la probabilité que cette équipe ait trouvé au moins une clé ?
" au moins une clé" signifie : une ou deux clés.
Probabilité de ne pas trouver de clé dans la première balise : un
cas favorable sur 3 possibilités, donc 1 /3.
Dans l'hypothèse ou l'on a pas trouver de clé dans la première balise :
probabilité de trouver une clé dans la
seconde balise : deux cas favorables sur 2 possibilités, donc
événement certain.
Probabilité de trouver au moins une clé : 1 -1/3 = 2 /3.
|
|