Mathématiques,
brevet 2017 Pondichéry
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
....
.....
|
Exercice 1. ( 5 points)
On considère l'expression E = (x-2)(2x+3)-3(x-2)
1. Développer E.
E = 2x2+3x-4x-6-3x+6
E =2x2-4x.
2. Factoriser E et
vérifier que E = 2 F avec F = x(x-2).
E = (x-2) [(2x+3)-3] = (x-2)2x = 2 [x(x-2)] = 2 F.
3. Déterminer
tous les nombres x tels que E = 0.
Pour qu'un produit de facteurs soit nul, il suffit que l'un des
facteurs soit nul.
x = 0 et x-2 = 0 soit x=2.
Exercice
2. (6 points)
Un sac contient 20 boules ayant chacune la même probabilité d'être tirée.
Ces boules sont numérotées de 1 à 20. On tire une boule au hasard dans
le sac.
1. Quelle est la probabilité de
tirer la boule numérotée 13 ?
1 cas favorable sur 20 possibilités . La probabilité de tirer la boule
n°13 est 1 / 20 = 0,05.
2. Quelle est la
probabilité de tirer une boule portant un numéro paire ?
10
cas favorables (2 ; 4 ; 6 ; 8 ; 10 ; 12 ; 14 ; 16 ; 18 ; 20) sur 20
possibilités . La probabilité de tirer une boule portant un numéro pair
est 10 / 20 = 0,5.
3.A-t-on
plus de chance d'obtenir une boule portant un numéro multiple de 4 que
d'obtenir une boule portant un numéro diviseur de 4 ?
Les multiples de 4 sont 4 ; 8 ; 12 ; 16 ; 20.
Probabilité de tirer une boule portant un numéro multiple de 4 : 5 /20
= 0,25.
Les diviseurs de 4 sont : 4 ; 2 ; 1.
Probabilité de tirer une boule portant un
numéro diviseur de 4 : 3 /20 = 0,15.
On plus de chance d'obtenir une boule
portant un numéro multiple de 4 que d'obtenir une boule portant un
numéro diviseur de 4.
4. Quelle est la probabilité de
tirer une boule portant un numéro qui soit un nombre premier ?
Nombres premiers : 2 ; 3 ; 5 ; 7 ; 11 ; 13 ; 17 ; 19.
La probabilité de tirer une boule portant
un numéro qui soit un nombre premier est : 8 / 20 = 0,4.
Exercice 3.(
7 points )..
On considère le programme de calcul suivant dans lequel Etape1, Etape2
et Résultat sont quatre variables.
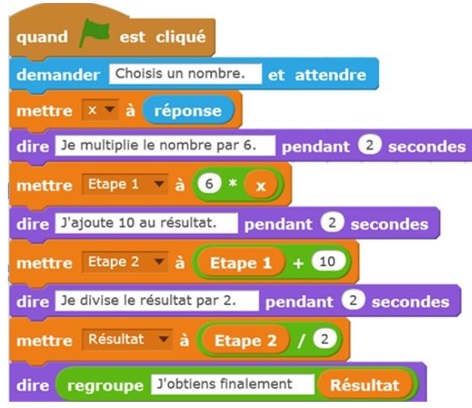
1.a. Julie a fait
fonctionner ce programme en choisissant le nombre 5. Vérifier que ce
qui est dit à la fin est " j'obtiens finalement 20".
5 x6 =30 ; 30+10=40 ; 40 /2 =20.
1.b. Que dit le
programme si Julie le fait fonctionner en choississant au départ le
nombre 7 ?
7 x6 = 42 ; 42 +10 = 52 ; 52 / 2 = 26.
2.
Julie a fait fonctionner ce programme. Ce qui est dit à la fin est "
jobtiens finalement 8". Quel nombre Julie a-t-elle choisi au départ ?
8 x2 = 16 ; 16-10 = 6 ; 6 /6 =1.
3. Si on appelle x
le nombre choisi au départ, écrire en fonction de x l'expression
obtenue à la fin du programme, puis réduire cette expression autant que
possible.
(6x +10 ) / 2 = 3x +5.
4. Maxime utilise
le programme de calcul ci-dessous :
Choisir un nombre ;
lui ajouter 2 ;
multiplier le résultat par 5.
Peut-on choisir un nombre pour lequel le résultat obtenu par maxime est
le même que celui de Julie ?
Maxime :5(x+2) ; Julie : 3x+5.
5x +10 = 3x +5 ; 5x-3x = 5-10 ; 2x = -5 ; x = -2,5.
|
|
|
|
Exercice 4. ( 7
points )
Pour
ses 32 ans, Denis a acheté un vélo d'appartement afin de pouvoir
s'entraîner pendant l'hiver. La fréquence cardiaque ( FC) est le nombre
de pulsations ( ou battements) du coeur par minute.
1. Denis veut
estimer sa fréquence cardiaque : en 15 s, il a compté 18 pulsations. A
quelle fréquence cardiaque, exprimée en pulsations par minute, cela
correspond-il ?
18 x 60 / 15 = 72.
2. Son vélo
est équipé d'un cardiofréquencemètre qui lui permet d'optimiser son
effort en enregistrant dans ce cardiofréquencemètre, toutes les
pulsations de son coeur. A un moment donné, le cardiofréquencemètre a
mesuré un intervalle de 0,8 s entre deux pulsations. Calculer la
fréquence cardiaque qui sera affichée par le cardiofréquencemètre.
60 / 0,8 = 75.
3. Après une séance
d'entraînement, le cardiofréquencemètre a fourni les renseignements
suivants :
Nombre de pulsations enregistrées : 3640 ; fréquence minimale : 65
pulsations / minute ; fréquence moyenne : 130 pulsations / minute ;
fréquence maximale : 182 pulsations par minute.
a. Quelle est
l'étendue des fréquences cardiaques enregistrées : 182 -65 = 117.
b. Quelle est la
durée de l'entraînement ?
3640 / 130 =28 min.
4.
Denis souhaite connaître sa fréquence cardiaque maximale conseillée (
FCMC) afin de ne pas la dépasser et ainsi ménager son coeur. La FCMC
d'un individu dépend de son âge a, exprimé en années, elle peut
s'obtenir grâce à la formule suivante : FCMC =f(a)= 220 -a.
a. Vérifier que la
FCMC de Denis est égale à 188 pulsations / minute.
220-32=188.
b. Comparer la FCMC
de Denis avec celle d'une personne de 15 ans.
220-15 = 205 ; la FCMC de Denis est infrieure à celle d'une personne de
15 ans.
5. Après quelques recherches, Denis trouve une autre formule de calcul
de la FCMC, plus précise.
FCMC =g(a)= 191,5 -0,007 a2.
Denis utilise un tableur pour comparer les résultats obtenus à l'aide
des deux formules.
|
A
|
B
|
C
|
1
|
Age
a
|
FCMC
f(a)
|
FCMC
g(a)
|
2
|
30
|
190
|
185,2
|
3
|
31
|
189
|
184,773
|
4
|
32
|
188
|
184,332
|
5
|
33
|
187
|
183,877
|
Quelle formule faut-il insérer dans le
cellule C2 puis recopier vers le bas, pour pouvoir compléter la colonne
FCMC g(a).
=191,5-0,007*A2^2 ou =191,5-0,007*A2*A2
Exercice 5. (8 points)
Un térawattheure est noté 1TWh.
La géothermie permet la production d'énergie électrique grâce à la
chaleur des nappes d'eau souterraines. Le graphique ci-dessous
représente les production d'électricité par différentes sources
d'énergie en France en 2014.
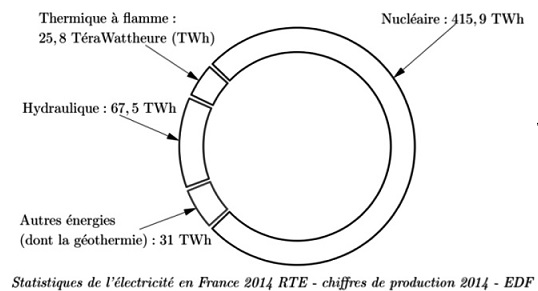
1.a. Calculer la
production totale d'électricité en France en 2014..
415,9 +25,8 +67,5 +31 = 540,2 TWh.
b. Montrer que la
proportion d'énergie électrique produite par les autres énergies ( dont
la géothermie ) est environ égale à 5,7 %.
31 x100 / 540,2 ~5,7 %.
2. Le table u suivant présente les production d'électricité
par les différentes sources d'énergie, en France, en 2013 et 2014.
|
Thermique
à flamme
|
Hydraulique
|
Autres
énergies
dont géothermie
|
Nucléaire
|
2013
( TWh)
|
43,5
|
75,1
|
28,1
|
403,8
|
2014
(TWh)
|
25,8
|
67,5
|
31
|
415,9
|
Variation
( %)
|
-40,7
|
-10,1
|
+10,3
|
+3
|
...Alice et Tom ont discuté pour savoir quelle est la source d'énergie
qui a le plus augmenté sa production d'électricité. Tom pense qu'il
s'agit des autres énergies et Alice pense qu'il s'agit du nucléaire.
Quel est le raisonnement tenu par chacun d'eux ?
Tom a regardé la variation en pourcentage : +10,3 % alors que
l'augmentation est seulement de 31-28,1 =2,9 TWh.
Alice a calculé l'augmentation 415,9 -403,8 = 12,1 TWh. Elle ne
s'est pas contentée de regarder le pourcentage de variation.
3. La centrale
géothermique de Rittershoffen a été inaugurée en 2016. On y a creusé un
puits pour capter l'eau chaude sous pression, à 2500 m de profondeur, à
une température de 170°C.
Ce puits à la forme d'un tronc de cône représenté ci-dessous. Les
proportions ne sont pas respectées. On calule le volume du tronc de
cône grâce à la formule suivante :
V = p/3 h (R2+R
r +r2)
h : hauteur, R rayon de la grande base et r rayon de la petite base.
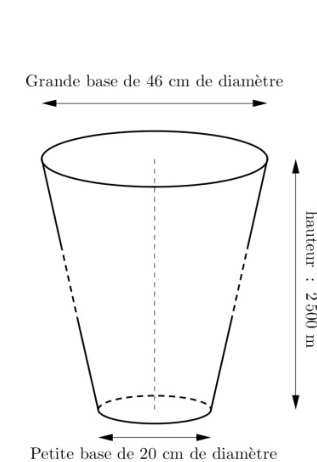
a. Vérifier que le
volume du puits est environ 225 m3.
V = 3,14 / 3 x2500 (0,232 +0,23 x0,10 +0,102)~225
m3.
b. La terre est
tassée quand elle est dans le sol. Quand on l'extrait, elle n'est plus
tassée et son volume augmente de 30 %. Calculer le volume final de
terre à stocker après le forage du puits.
225 x1,3 ~292,5 m3.
|
|
Exercice 6. ( 7 points)
On
obtient la pente d'une route en calculant le quotient du dénivelé (
déplacement vertical / déplacement horizontal ) Une pente s'exprime
sous forme de pourcentage.
Classer les pentes suivantes dans l'ordre décroissant.

Exercice 7. (5 points)
Alban souhaite proposer sa candidature pour un emploi. Il doit envoyer
dans une seule enveloppe : 2 copies de sa lettre de
motivation et 2 copies de son CV. Chaque copie est rédigée sur une
feuille au format A4.
1. Il souhaite faire partir son
courrier en lettre prioritaire. Pour déterminer le
prix du timbre, il obtient la grille de tarif d'affranchissement
suivante.
Le tarif est-il proportionnel à la masse ?
Non, le rapport masse / tarif n'est pas constant.
Masse
(g) jusqu'à
|
20
|
100
|
250
|
500
|
3000
|
Tarif
(€)
|
0,80
|
1,60
|
3,20
|
4,80
|
6,40
|
masse
/ tarif
|
25
|
62,5
|
78,12
|
104,17
|
468,75
|
2. Afin de choisir le bon tarif, il
réunit les informations suivantes :
Masse d'un paquet de 50 enveloppes : 175 g.
Dimension d'une feuille A4 : 21 cm x 29,7 cm.
Grammage d'une feuille A4 : 80 g / m2. 1 m2 = 104
cm2.
Quel tarif doit-il choisir ?
Masse d'une enveloppe : 175 / 50 = 3,5 g.
Masse d'une feuille A4 : 80 x0,21 x0,297 =4,99 g.
Masse de 4 feuilles A4 : 4 x4,99 ~19,96 g.
Masse totale : 3,5 +19,96 =23,46 g.
La masse est comprise entre 20 g et 100 g : tarif : 1,60 €.
|
|
|
|