Mathématiques,
Diplome national du brevet, Polynésie septembre 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
Exercice 1. 9 points. Sur
une feuille de calcul, on a reporté le classement des dix premiers
pays, par le nombre de médailles, aux Jeux Olympiques de Rio en 2016.
|
A
|
B
|
C
|
D
|
E
|
F
|
1
|
Rang
|
Pays
|
Or
|
Argent
|
Bronze
|
Total
|
2
|
1
|
Etats-Unis
|
46
|
37
|
38
|
121
|
3
|
2
|
Grande Bretagne |
27
|
23
|
17
|
67
|
4
|
3
|
Chine
|
26
|
18
|
26
|
70
|
5
|
4
|
Russie
|
19
|
18
|
19
|
56
|
6
|
5
|
Allemagne
|
17
|
10
|
15
|
42
|
7
|
6
|
Japon
|
12
|
8
|
21
|
41
|
8
|
7
|
France
|
10
|
18
|
14
|
42
|
9
|
8
|
Corée du Sud
|
9
|
3
|
9
|
21
|
10
|
9
|
Italie
|
8
|
12
|
8
|
28
|
11
|
10
|
Australie
|
8
|
11
|
10
|
29
|
1. Quelle formule,
parmi les trois proposées, a été saisie dans la cellule F2 de cette
feuille de calcul, avant qu’elle soit étirée vers le
=46+37+38
=SOMME(C2 :E2) Vrai.
C2+D2+E2
2. On observe la série des nombres de médailles d'or de ces dix pays.
a. Quelle est l'étendue de cette série ?
46-8 = 38.
b. Quelle est la moyenne de cette série ?
(46 +27 +26 +19 +17 +12 +10 +9 +8 +8 ) / 10 =18,2 ~ 18.
3. Quel est le
pourcentage de médailles d'or remportées par la France par rapport à
son nombre total de médailles ? Arrondir le résultat au dixième de %.
10 / 42 x100 ~ 23,8 %.
4. Le classement
aux Jeux Olympiques s’établit selon le nombre de médailles d’or
obtenues et non selon le nombre total de médailles. Pour cette raison,
la France avec 42 médailles se retrouve derrière le Japon qui n’en a
que 41. En observant l’Italie et l’Australie, établir la règle de
classement en cas d’égalité sur le nombre de médailles d’or.
En cas d'égalité sur le nombre de médailles d'or, on regarde le nombre
de médailles d'argent. Le pays qui en a le plus est d'abord classé.
En cas d'égalité sur le nombre de médailles d'or et d'argent,
on regarde le nombre de médailles de bronze. Le pays qui en a le plus
est d'abord classé.
5. Un journaliste
sportif propose une nouvelle procédure pour classer les pays : chaque
médaille d’or rapporte 3 points, chaque médaille d’argent rapporte 2
points et chaque médaille de bronze rapporte 1 point. Dans ces
conditions, la France dépasserait-elle le Japon ?
France : 30 +36+14 =80 ; Japon : 36+16 +21=73. La France dépasserait le Japon.
Exercice 2. 10 points
Le 17 juillet 2016, une spectatrice regarde l'étape « Bourg-en-Bresse / Culoz » du Tour de France.
Elle note, toutes les demi-heures, la distance parcourue par le
cycliste français Thomas VOECKLER qui a mis 4 h 30 min pour parcourir
cette étape de 160 km ; elle oublie seulement de noter la distance
parcourue par celui-ci au bout de 1 h de course.
Elle obtient le tableau suivant :
Temps (h)
|
0
|
0,5
|
1
|
1,5
|
2
|
2,5
|
3
|
3,5
|
4
|
4,5
|
Distance (km)
|
0
|
15
|
...
|
55
|
70
|
80
|
100
|
110
|
135
|
160
|
1. Quelle distance a-t-il parcourue au bout de 2 h 30 min de course ?
80 km.
2. Montrer qu’il a parcouru 30 km lors de la troisième heure de course.
30-70 = 30 km.
3. A-t-il été plus rapide lors de la troisième ou bien lors de la quatrième heure de course ?
Lors de la quatrième heure, il a parcouru 135-100 = 35 km. Il a été plus rapide que durant la troisième heure.
4. Répondre aux questions qui suivent.
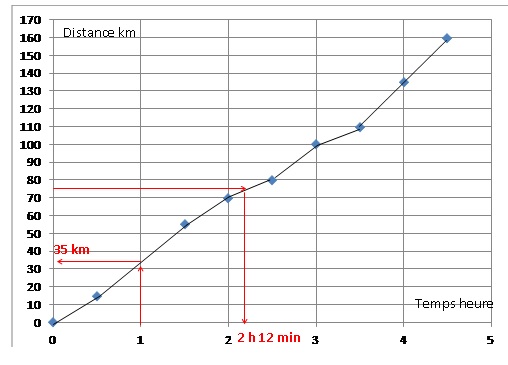
a. Placer les 9 points du
tableau dans le repère. On ne peut pas placer le point d’abscisse 1
puisque l’on ne connaît pas son ordonnée.
b. En utilisant votre règle, relier les points consécutifs entre eux.
5. En considérant que la
vitesse du cycliste est constante entre deux relevés, déterminer, par
lecture graphique, le temps qu’il a mis pour parcourir 75 km.
6. On considère que la vitesse
du cycliste est constante entre le premier relevé effectué au bout de
0,5 h de course et le relevé effectué au bout de 1,5 h de course ;
déterminer par lecture graphique la distance parcourue au bout de 1 h
de course.
7. Soit f la fonction, qui au
temps de parcours du cycliste Thomas VOECKLER, associe la distance
parcourue. La fonction f est-elle linéaire ?
Non, le graphe n'est pas une droite passant par l'origine.
|
|
| ... |
|
|
Exercice 3. 6 points
Le jardinier d’un club de football décide de semer à nouveau du gazon
sur l’aire de jeu. Pour que celui-ci pousse correctement, il installe
un système d'arrosage automatique qui se déclenche le matin et le soir,
à chaque fois, pendant 15 minutes.
Le système d’arrosage est constitué de 12 circuits indépendants.
Chaque circuit est composé de 4 arroseurs.
Chaque arroseur a un débit de 0,4 m3 d'eau par heure.
Combien de litres d'eau auront été consommés si on arrose le gazon pendant tout le mois de juillet ?
On rappelle que 1 m3 = 1 000 litres et que le mois de juillet compte 31 jours.
48 arroseurs débitent : 48 x0,4 = 19,2 m3 d'eau par heure.
19,2 x0,5 = 9,6 m3 d'eau par jour.
9,6 x31 =297,6 m3 (297 600 L ) d'eau en juillet.
Exercice 4. 7 points.
La figure ci-dessous représente le plan de coupe d’une tribune d’un
gymnase. Pour voir le déroulement du jeu, un spectateur du dernier rang
assis en C doit regarder au-dessus du spectateur placé devant lui et
assis en D. Une partie du terrain devant la tribune lui est alors
masquée. On considèrera que la hauteur moyenne d’un spectateur assis
est de 80 cm (CT = DS = 80 cm).
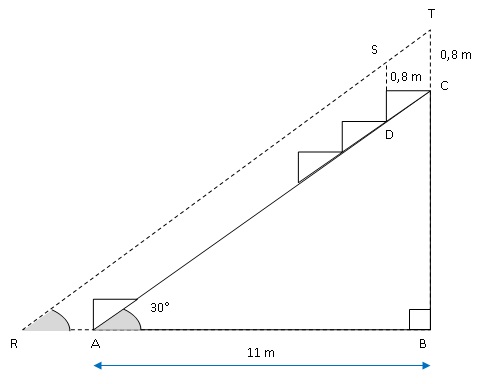
Sur ce plan de coupe de la tribune :
les points R, A et B sont alignés horizontalement et les points B, C et T sont alignés verticalement ;
les points R, S et T sont alignés parallèlement à l’inclinaison (AC) de la tribune ;
on considérera que la zone représentée par le segment [RA] n’est pas visible par le spectateur du dernier rang ;
la largeur au sol AB de la tribune est de 11 m et l’angle BAC d’inclinaison de la tribune mesure 30°.
1. Montrer que la hauteur BC de la tribune mesure 6,35 m, arrondie au centième de mètre près.
tan 30° = BC / AB ; BC = AB tan 30 = 11 x0,577 ~6,35 m.
2. Quelle est la mesure de l’angle BRT ?
Les droites (RT) et (AC) étant parallèles, cet angle mesure 30°.
3. Calculer la longueur RA en centimètres. Arrondir le résultat au centimètre près.
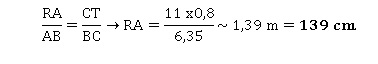
|
|
|
|
Exercice 5. 7 points
L’épreuve
du marathon consiste à parcourir le plus rapidement possible la
distance de 42,195 km en course à pied. Cette distance se réfère
historiquement à l’exploit effectué par le Grec PHILLIPIDÈS, en 490 av.
J-C, pour annoncer la victoire des Grecs contre les Perses. Il s’agit
de la distance entre Marathon et Athènes.
1. En 2014, le
kényan Dennis KIMETTO a battu l’ancien record du monde en parcourant
cette distance en 2 h 2 min 57 s. Quel est alors l’ordre de grandeur de
sa vitesse moyenne : 5 km/h, 10 km/h ou 20 km/h ?
~ 20 km / h.
2. Lors de cette
même course, le britannique Scott OVERALL a mis 2 h 15 min pour
réaliser son marathon. Calculer sa vitesse moyenne en km/h. Arrondir la
valeur obtenue au centième de km/h.
2 h 15 min = 2,25 h ; vitesse moyenne = 42,195 / 2,25 ~18,75 km / h.
3. Dans cette
question, on considérera que Scott OVERALL court à une vitesse
constante. Au moment où Dennis KIMETTO franchit la ligne d’arrivée,
déterminer :
a. le temps qu’il reste à courir à Scott OVERALL ;
b. la distance qu’il lui reste à parcourir. Arrondir le résultat au mètre près.
Différence de temps : 2 h 15 min = 2 x3600 +15 x60 = 8100 s.
2 h 2 min 57 s = 7200 +120 +57 = 7377 s.
8100-7377= 723 s.
vitesse moyenne 18,75 / 3,6 ~5,21 m /s.
Distance restante à courir : 5,21 x 723 ~3766 m.
Exercice 6. 5
points.
La figure ci-après est la copie d’écran d’un programme réalisé avec le logiciel « Scratch ».

1. Montrer que si on choisit 2 comme nombre de départ, alors le programme renvoie −5
2 x2 -9 =4-9 = -5.
2. Que renvoie le programme si on choisit au départ :
a. le nombre 5 ?
5 x 5 -9 =25-9 =16.
b. le nombre −4 ?
-4 x (-4) -9 = 16-9 =7.
3. Déterminer les nombres qu’il faut choisir au départ pour que le programme renvoie 0.
x2-9 =0 ; x =3 et x = -3.
|
|
|