Géométrie, mesure d'angle, Thalès, Phytagore, brevet 2013

Géométrie, mesure d'angle, Thalès, Phytagore, brevet 2013.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

(sujet 2013)
Trois figures codées sont données ci-dessous. Elles ne sont pas dessinées en vraie grandeur.
Pour chacune d’elles, déterminer la mesure de l’angle ABC.

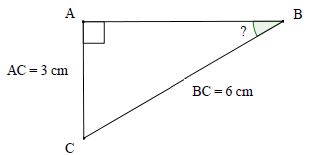
sin ABC = AC / BC = 3 / 6 = 0,5 ; l'angle ABC mesure 30°.

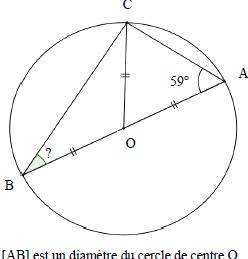
Le triangle ABC, inscrit dans un cercle de diamètre AB est rectangle en C. L'angle ABC est le complémentaire de l'angle CAB. l'angle ABC mesure 90-59 = 31°.

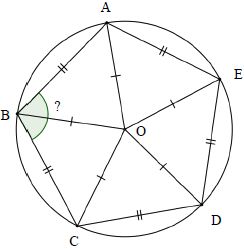
Le pentagone est inscrit dans un cercle. L'angle au centre AOB mesure 360/5 = 72 °.
Le triangle AOB est isocèle. L'angle ABO mesure : ½(180-72) =54°. L'angle ABC mesure : 2*54 = 108 °.

.
.

Pascal souhaite déterminer la hauteur d'un cône de sel de diamètre 5 mètres. Il possède un bâton de longueur 1 mètre. Il effectue des mesures et réalise le schéma ci-dessous :

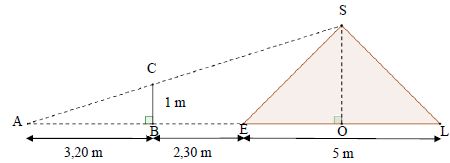
Démontrer que la hauteur de ce cône de sel est égale à 2,50 mètres.
Relation de Thalès dans les triangles ABC et AOS : AB / AO = BC / OS.
Soit OS = BC * AO / AB =1*(3,2+2,3+2,5) / 3,2 = 2,50 m.
A l’aide de la formule V=1/3 pR²H, déterminer, en m³, le volume de sel contenu dans ce cône. Arrondir le résultat au m³ près.
V = 3,14 / 3 * 2,5²*2,5=16,36 ~16 m³.
Le sel est ensuite stocké dans un entrepôt sous la forme de cônes de volume 1 000 m³. Par mesure de sécurité, la hauteur d'un tel cône de sel ne doit pas dépasser 6 mètres. Quel rayon faut-il prévoir au minimum pour la base ? Arrondir le résultat au décimètre près
R² = 3 V / (pH) = 3000/(3,14*6)=159,155 m² ;
prendre la racine carée : R ~ 12,6 m.

.

Moana a d'abord posé sur le sol, à partir du cocotier, des noix de coco régulièrement espacées à chacun de ses pas, puis il i'est ensuite placé exactement comme indiqué sur le croquis, au niveau dela7" noix de coco. Moana mesure 1,8 m et fait 111 pas pour parcourir 100 m.

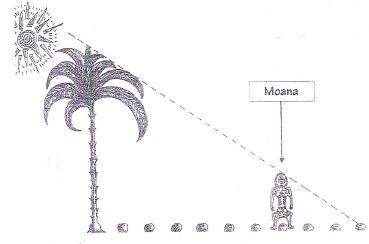
Calcule la hauteur H du cocotier.
Relation de Thalès : H/1,8 = 10 / 7 ; H = 18/7 =2,57 m.

La ville BONVIVRE possède une plaine de jeux bordée d’une piste cyclable. La piste cyclable a la forme d’un rectangle ABCD dont on a « enlevé trois des coins ». Le chemin de G à H est un arc de cercle ; les chemins de E à F et de I à J sont des segments. Les droites (EF) et (AC) sont parallèles.

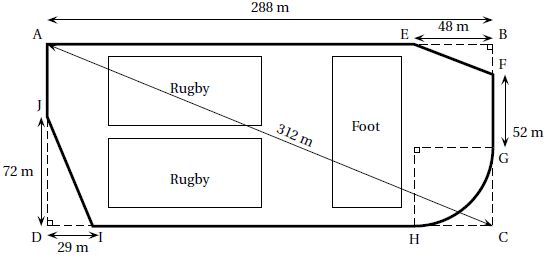
Quelle est la longueur de la piste cyclable ? Justifier la réponse.
L= AE + EF +FG+arc GH +HI +IJ +IA.
AE = 288-48 = 240 m ;
Pythagore dans le triangle rectangle ABC : BC² +AB² = AC² ; BC² = AC² -AB² =312²-288² = 14400 ; BC =120 m.
Thalès dans les triangles EBF et ABC : EB / AB = BF / BC ; BF = EB *BC / AB = 48*120 / 288=20 m.
Phytagore dans le triangle rectangle EBF : EF² = BE² + BF² = 48² +20² =2704 ; EF = 52 m.
Rayon de l'arc de cercle GH : R =BC-BF-EG = 120-20-52=48 m ; longueur de cet arc : pR/2 = 75,4 m.
IH = AB-DI-HC =288-29-48=211 m.
Phytagore dans le triangle rectangle DIJ : IJ² = DJ² + DI² = 72² +29² =6025 ; IJ = 77,6 m.
AI = BC-DJ = 120-72 = 48 m.
L = 240 + 52 + 52 +75,4 + 211 + 77,6 + 48 = 756 m.

Construis un triangle ABC rectangle en C tel que AB : 10 cm et AC : 8 cm.
Calcule la longueur BC.

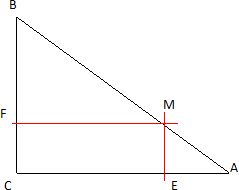
Phytagore dans le triangle rectangle ABC : AB² = AC² + BC² ; BC² = AB² - AC² = 10²-8² =36 ; BC = 6 cm.
Place le point M de I'hypoténuse [AB] tel que AM = 2 cm. Trace la perpendiculaire à [AC] passant par M. Elle coupe [AC] en E.
Trace la perpendiculaire à [BC] passant par M. Elle coupe [BC] en F.
Comment prouver que le quadriiatère MFCE est un rectangle.
L'angle C est droit ; ME est perpendiculaire à AC : l'angle E est droit.
MF est perpendiculaire à BC : l'angle F est droit.
Si un quadrilatère a 3 angles droits alors c'est un rectangle.

On considère un triangle ABC isocèle en A tel que l’angle� BAC mesure 50° et AB est égal à 5 cm. On note O le centre du cercle circonscrit au triangle ABC. La droite (OA) coupe ce cercle,
noté (C), en un autre point M.

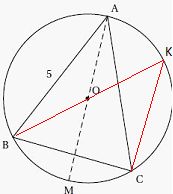
Quelle est la mesure de l’angle �BAM ?
Le centre du cercle circonscrit est le point de concours des médiatrices. La droite AM est la médiatrice de [BC], c'est donc un axe de symétrie de la figure. par suite l'angle BAM mesure la moitié de l'angle BAC, c'est à dire 25°.
Quelle est la nature du triangle BAM ? Justifier.
AM est un diamètre du cercle ; le triangle BAM est inscrit dans un demi-cercle. Le triangle BAM est rectangle en B.
Calculer la longueur AM et en donner un arrondi au dixième de centimètre près.
Dans le triangle rectangle BAM : cos 25 = AB / AM ; AM = AB / cos 25 = 5 / cos 25 = 5,5 cm.
La droite (BO) coupe le cercle (C) en un autre point K. Quelle est la mesure de l’angle �BKC ? Justifier.
Les angles BAC et BKC sont inscrits et interceptent le même arc de cercle BMC. Ces deux angles ont donc la même mesure, 50°.

BCDE est un carré de 6 cm de côté. Les points A, B et C sont alignés et AB = 3 cm.
F est un point du segment [CD]. La droite (AF) coupe le segment [BE] enM.
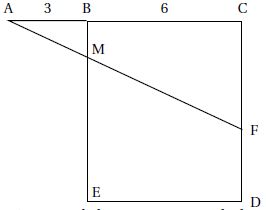La figure n'est pas à l'échelle.
Déterminer la longueur CF par calcul ou par construction pour que les longueurs BMet FD soient égales.
Thalès dans les triangles ACF et ABM : AC / AB =3= CF / BM = (CD-FD) / BM.
3 BM =CD-FD = 6-BM ; 4 BM = 6 ; BM = 1,5 cm.

.

menu