Géométrie : calculs d'aire et de volume, brevet 2013. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . (sujet 2013) Sur un parking, une commune veut regrouper 6 conteneurs à déchets du même modèle A ou B. Les deux modèles sont fabriqués dans le même matériau qui a partout la même épaisseur. 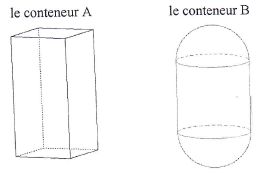- le conteneur A est un pavé droit à base carrée de côté a=1 m, et de hauteur h=2 m - le conteneur B est constitué de deux demi-sphères de rayon r=0,58 m et d'un cylindre de même rayon et de hauteur H=1,15 m Vérifie que les 2 conteneurs ont pratiquement le même volume. VA = aire de base  fois hauteur = a2h = 12*2 = 2 m3. VB = aire cylindre + aire sphère = pr2H + 4/3 pr3. VB =3,14*0,582*1,15 +4/3*3,14*0,583 =2 m3. Quels peuvent être les avantages du conteneur A ? Le conteneur A tient mieux sur le sol, alors que B peut basculer. Par contre A est trop haut et donc difficile d'accès. On souhaite savoir quel est le conteneur le plus économique à fabriquer.  Calcule I'aire totale des 6 faces du conteneur A. A = 2a2 + 4ah =2+4*1*2 = 10 m2. Vérifie que, pour le conteneur B, l'aire totale, arrondie à 0,1 m2 près, est 8,4 m2. aire d'une sphère + aire latérale du cylindre = 4pr2 +2prH =4*3,14*0,582 + 2*3,14*0,58*1,15 =8,4 m2. Quel est le conteneur le plus économique à fabriquer ? Justifie ta réponse. Il faut moins de matière pour fabriquer le conteneur B : ce dernier est donc le plus économique. . . Pascal souhaite déterminer la hauteur d'un cône de sel de diamètre 5 mètres. Il possède un bâton de longueur 1 mètre. 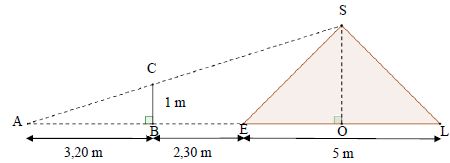Il effectue des mesures et réalise le schéma ci-dessous : Démontrer que la hauteur de ce cône de sel est égale à 2,50 mètres. Relation de Thalès dans les triangles ABC et AOS : AB / AO = BC / OS. Soit OS = BC * AO / AB =1*(3,2+2,3+2,5) / 3,2 = 2,50 m. A l’aide de la formule V=1/3 pR2H, déterminer, en m3, le volume de sel contenu dans ce cône. Arrondir le résultat au m3 près. V = 3,14 / 3 * 2,52*2,5=16,36 ~16 m3. Le sel est ensuite stocké dans un entrepôt sous la forme de cônes de volume 1 000 m3. Par mesure de sécurité, la hauteur d'un tel cône de sel ne doit pas dépasser 6 mètres. Quel rayon faut-il prévoir au minimum pour la base ? Arrondir le résultat au décimètre près R2 = 3 V / (pH) = 3000/(3,14*6)=159,155 m2 ; prendre la racine carée : R ~ 12,6 m. . Un moule à muffins(2) est constitué de 9 cavités. Toutes les cavités sont identiques. Chaque cavité a la forme d’un tronc de cône (cône coupé par un plan parallèle à sa base) représenté ci-dessous. Les dimensions sont indiquées sur la figure. 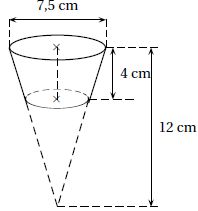Montrer que le volume d’une cavité est d’environ 125 cm3. Volume du grand cône de hauteur H =12 cm et de rayon R = 3,75 cm : V=1/3 pR2H =3,14/3*3,752*12=176,7 cm3. Hauteur du petit cône h = 12-4=8 cm. Rayon r du petit cône : la relation de Thalès conduit à : R/r = H/h ; r = Rh/H = 3,75*8/12=2,5 cm. Volume du petit cône de hauteur h =8 cm et de rayon r = 2,5 cm : V=1/3 pr2h =3,14/3*2,52*8=52,4 cm3. Puis : 176,7 -52,4 = 124,3 ~125 cm3. Léa a préparé 1 litre de pâte. Elle veut remplir chaque cavité du moule au 3/4 de son volume. A-t-elle suffisamment de pâte pour les 9 cavités du moule ? Justifier la réponse. Volume de pâte par cavité  : 125*3/4 =93,75 cm3 ; volume des 9 cavités : 9*93,75 ~844 cm3. Elle dispose de 1 L = 1000 cm3 de pâte, cela est bien suffisant pour le remplissage. On dispose d'un carré de métal de 40 cm de côté. Pour fabriquer cette boîte parallélépipédique, on enlève à chaque coin un carré de côté x et on relève les bords par pliage. 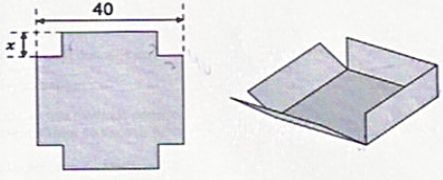Quelles sont les valeurs possibles de x ? x doit être inférieur à 20 cm.. Calculer le volume de la boîte pour x = 5 cm. Aire de la base, carré de 30 cm de côté : 30*30 = 900 cm2. Hauteur H = 5 cm ; volume de la boîte : 900*5 = 4500 cm3. 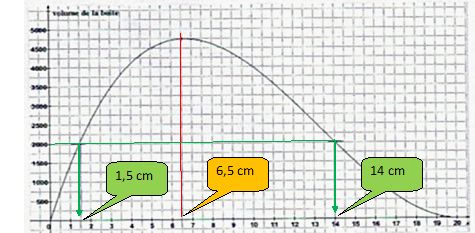Le graphe suivant donne le volume de la boîte en fonction de x. Pour quelle valeur de x, le volume est-il maximum ?  Quelles sont les valeurs possibles de x si le volume est 2000 cm3 ? ABCD est un trapèze et les longueurs sont données en cm.   Donner une méthode permettant de calculer l'aire du trapèze et la calculer. 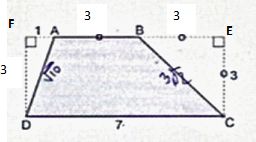Aire du trapèze =Aire du rectangle CDFE-aires des triangle rectangle FAD et BEC. A = 7*3 -0,5*1*3-0,5*3*3 =15 cm2. L'aire d'un trapèze est donnée par l'une des formules suivantes. 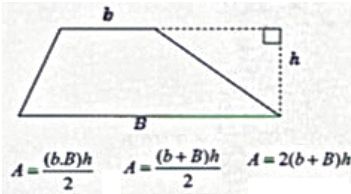Retrouver la formule en justifiant. Aire du trapèze =Aire du rectangle CDFE-aires des triangle rectangle FAD et BEC. A = B h -0,5 AF*h-0,5BE*h = h( B-0,5(AF+BE). Or AF+BE= B-b ; par suite : A = h ( B-0,5 B+0,5b) = 0,5 h(B+b). .

menu