Géométrie, Pythagore, Thalès, trigonométrie, brevet 2013

Géométrie, Pythagore, Thalès, trigonométrie, brevet 2013.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

(sujet 2013)
Sur le dessin ci-dessous, les points A, B et E sont alignés, et C le milieu de [BD].

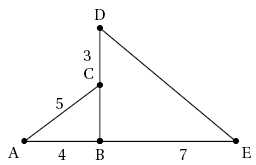
Quelle est la nature du triangle ABC ? Justifier.
AC² =25 ; AB²+BC² =16+9=25 ; donc AC² =AB²+BC².
Le triangle ABC est rectangle en B.
En déduire la nature du triangle BDE.
Le triangle BDE est rectangle en B
Calculer ED. Arrondir le résultat au dixième.
DE² =BE²+BD² = 49+36=85 ; DE ~9,2 cm.

En se retournant lors d’une marche arrière, le conducteur d’une camionnette voit le sol à 6 mètres derrière son camion.
Sur le schéma, la zone grisée correspond à ce que le conducteur ne voit pas lorsqu’il regarde en arrière.

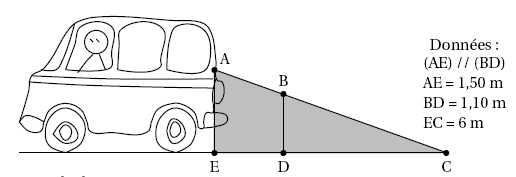
Calculer DC.
Les triangles EAC et DBC ont des côtés dont les mesures sont proportionnelles.
EC / CD = AE / BD ; CD = EC*BD / AE = 6*1,10 / 1,50 = 4,4 cm.
En déduire que ED = 1,60 m.
ED = EC-DE =6-4,4 = 1,6 m.
Une fillette mesure 1,10 m. Elle passe à 1,40 m derrière la camionnette. Le conducteur peut-il la voir ? Expliquer.
BD = 1,10 m ( hauteur de la filette) ; ED = 1,6 m, la filette de hauteur 1,10 m passe entre E et D, elle se trouve donc dans la zone grisée et le chauffeur ne la voit pas.

On souhaite construire une structure pour un skatepark, constituée d’un escalier de six marches identiques permettant d’accéder à un plan incliné dont la hauteur est égale à 96 cm. Le projet de cette structure est présenté ci-dessous.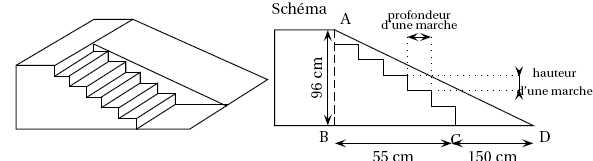

Normes de construction de l’escalier :
60 <= 2h + p <= 65 où h est la hauteur d’une marche et p la profondeur d’une marche, en cm.
Demandes des habitués du skate park :
Longueur du plan incliné (c’est-à-dire la longueur AD) comprise entre 2,20 m et 2,50 m.
Angle formé par le plan incliné avec le sol (ici l’angle� BDA) compris entre 20° et 30°.
Les normes de construction de l’escalier sont-elles respectées ?
6 h = 96 ; h = 96 / 6 = 16 cm ; 55 = 5 p ; p = 11 cm ; 2h+p = 43 cm.
Les normes de construction de l'escalier ne sont pas respectées.
Les demandes des habitués du skatepark pour le plan incliné sont-elles satisfaites ?
tan (BDA = AB / (BC+CD) =96 / (55+150)=0,468. L'angle BDA mesure 25°.
sin 25 = AB / AD ; AD = AB / sin 25 = 96 / sin 25 =227 cm = 2,27 m.
Les demandes concernant le plan inclinée sont satisfaites.

.
.

La figure ci-dessous représente un trapèze rectangle ABCD tel que :
AB = 12 cm; CD = 9 cm; BC = 5cm.

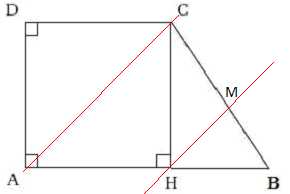
H est le pied de la hauteur issue de C.
Montrer que HB = 3 cm.
CD=AH=9 ccm ; HB=AB -AH = 12-9 = 3 cm.
Calculer CH.
BC² =CH²+HB² ; CH²= BC² -HB²=25-9=16 ; CH = 4 cm.
Déduire que le périmètre de ABCD est égal à 30 cm.
AB +BC +CD +DA = 12 + 5 +9 +4 =30 cm.
Calculer la mesure de l’angle� ABC au degré près.
tan ABC =CH / BH =4 / 3 = 1,33. L'angle ABC mesure 53°.
La parallèle à (AC) passant par H coupe la droite (BC) en M. Calculer BM.
Les triangles BHM et BAC ont des côtés dont les mesures sont proportionnelles.
BM / BC =BH / AB ; BM = BH*BC / AB = 3*5 /12 =1,25 cm.

.

Un après-midi, Juliette observe son poisson Roméo en se plaçant au dessus de son aquarium de forme sphérique. Elle remarque le drôle de manège de son poisson nageant à la surface :
• il part d’une paroi de l’aquarium et nage 12 cm avant d’atteindre à nouveau la paroi,
• il change alors de direction et nage encore 5 cm avant d’atteindre à nouveau la paroi se trouvant alors en un point diamétralement opposé à son point de départ,
• il rejoint directement son point de départ.
Le poisson effectue chaque déplacement en ligne droite.
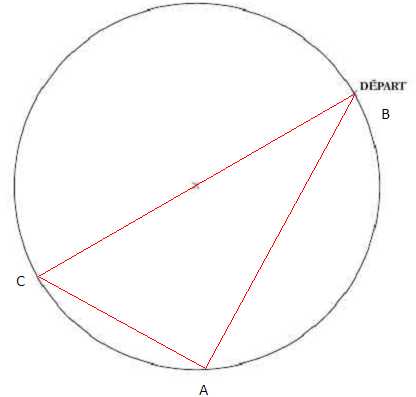
Représenter le déplacement de Roméo à la surface de l’eau, vu de dessus.

Quelle est la nature de la figure parcourue par Roméo ? Justifier.
B et C sont diamètralement opposés : BC est un diamètre du cercle.
Le triangle ABC est inscrit dans un demi-cercle : ce triangle est rectangle en A.
Calculer la distance totale parcourue par Roméo.
BC² =AB²+AC²=12²-5²=169 ; BC = 13 cm.
Distance parcourue : 12+5+13 = 30 cm.

Jean-Michel est propriétaire d’un champ, représenté par le triangle ABC ci-dessous. Il achète à son voisin le champ adjacent, représenté par le triangle ADC. On obtient ainsi un nouveau champ formé par le quadrilatère ABCD. Jean Michel sait que le périmètre de son champ ABC est de 154 mètres et que BC = 56 m.
Son voisin l’informe que le périmètre du champ ADC est de 144 mètres et que AC = 65 m. De plus, il sait que AD = 16 m.

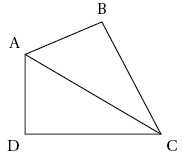
Justifier que les longueurs AB et DC sont respectivement égales à 33 m et 63 m.
AB +BC +AC = 154 ; AB = 154-BC-AC =154-56-65 =33 m.
AD +DC +CA = 144 m ; DC =144-DA-CA =144-16-65=63 m.
Calculer le périmètre du champ ABCD.
AB + BC +CD +DA = 33 +56 +63 +16 =168 m.
Démontrer que le triangle ADC est rectangle en D.
AC² =65² =4225 ; AD²+CD²=16² +63² =256+3969=4225.
AC² =AD²+CD² ; le riangle ADC est rectangle en D.
On admet que le triangle ABC est rectangle en B. Calculer l’aire du champ ABCD.
Aire du triangle ADC + aire du triangle ABC = ½AD*DC +½AB*BC =0,5(16*63 +33*56)=0,5(1008+1848) =1428 cm².
Jean-Michel veut clôturer son champ avec du grillage. Il se rend chez son commerçant habituel et tombe sur l’annonce suivante : Grillage : 0,85 € par mètre.
Combien va-t-il payer pour clôturer son champ ?
168*0,85 =142,8 €.

Voici le parcours du cross du collège La Bounty schématisé par la figure ci-dessous :

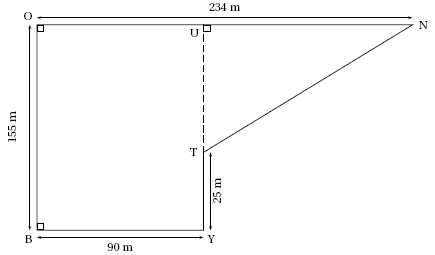
Montrer que la longueur NT est égale à 194 m.
NT² = UT²+UN² =(155-25)² +(234-90)² =16900+20736 =37636 ; NT =194 m.
Le départ et l’arrivée de chaque course du cross se trouvent au point B.
Calculer la longueur d’un tour de parcours.
L =234 +194 +25 +90 +155 =698 m.
Les élèves de 3^e doivent effectuer 4 tours de parcours. Calculer la longueur totale de leur course.
4*698 =2792 m.
Terii, le vainqueur de la course des garçons de 3^ème a effectué sa course en 10 minutes et 42 secondes.
Calculer sa vitesse moyenne et l’exprimer en m/s. Arrondir au centième près.
10 min 42 s = 10*60+42 = 642 s.
v_moy = 2792 / 642 =4,35 m/s.
Si Terii maintenait sa vitesse moyenne, penses-tu qu’il pourrait battre le champion Georges Richmond qui a gagné dernièrement la course sur 15 km des Foulées du Front de mer en 55 minutes et 11 secondes ?
Il va parcouir 15 km = 15000 m pendant : 15000 / 4,35 =3449 s soit 57 min 29 s. La réponse est Non.

Teiki se promène en montagne et aimerait connaître la hauteur d’un Pinus (ou Pin des Caraibes) situé devant lui. Pour cela, il utilise un bâton et prend quelques mesures au sol. Il procède de la façon suivante :
Il pique le bâton en terre, verticalement, à 12 mètres du Pinus. La partie visible (hors du sol) du bâton mesure 2 m.
Teiki se place derrière le bâton, de façon à ce que son oeil, situé à 1,60 m au dessus du sol, voie en alignement le sommet de l’arbre et l’extrémité du bâton.
Teiki marque sa position au sol, puis mesure la distance entre sa position et le bâton. Il trouve alors 1,2 m.
On peut représenter cette situation à l’aide du schéma ci-dessous :

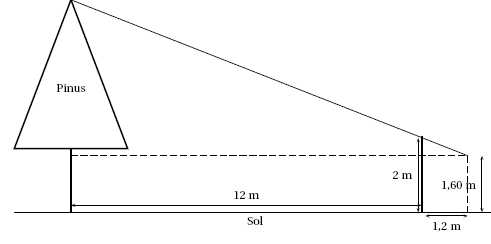
Quelle est la hauteur H du Pinus au-dessus du sol ?
(H-1,6) / (2-1,6) =(12+1,2) / 1,2 = 11 ; H-1,6 = 11(2-1,6) =4,4 m ; H = 4,4 +1,6 = 6 m.

menu