Evolution au cours du temps de la température de surface des inlandsis, concours général physique 2022.

Principe de la mesure de la température avec un thermistor.
On descend une sonde de température dans un trou de plusieurs centaines de mètres de profondeur, foré dans la glace. Le thermistor est un dipôle assimilable à une résistance R₀ dont la valeur dépend de sa température.
Le thermistor est placé dans le montage suivant :

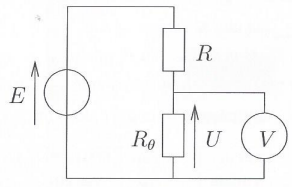
E est vosine de 1 V. Le voltmèrtre se comporte comme une résistance R_V.
47 . Exprimer la tension U en fonction de E, R, R_V et R₀.
Résistance équivalente à R₀ et R_V : R_équi = R₀R_V / (R₀+R_V).
E = (R+R_équi) I = RI +U ; I = (E-U) / R.
U = R_équi I =R_équi(E-U) / R.
U[1+R_équi / R) = R_équi E / R.
U[R+R_équi ] / R = R_équi E / R.
U[R+R_équi ] = R_équi E.
U = R_équi E / [R+R_équi ].
U =E / (R / R_équi +1] =E / [R(R₀+R_V) / ( R₀R_V)+1]
.
48. En pratique R_V >> R₀. Montrer que R₀ = U R / (E-U).
Quel est l'intérêt de se placer dans cette condition ?
Tracer l'allure de R₀ en fonction de U.
U ~E / [RR_V / ( R₀R_V)+1] = E / (R / R₀+1)= R₀E /(R+R₀).
UR + UR₀ = ER₀ ; R₀ = U R / (E-U).
L'introduction du voltmètre de grande résistance ne modifie par l'intensité.

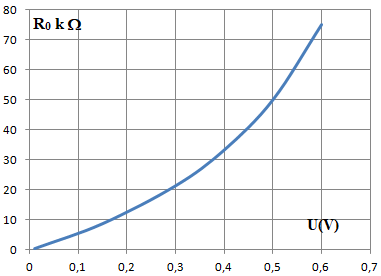
49. Commenter la relation obtenue à la question 48 dans les cas R₀ >> R, puis R₀ << R, enfin R=R₀. Dans quel(s) cas a t-on intérët
à se placer expérimentalement ?
R₀ >> R : U est voisine de E.
R₀ << R : U est voisine de 0.
R proche de R₀ : U est vosine de 0,5 E. Dans ce dernier cas on dispose d'une plus grande marge de mesures.
50 Pourquoi a t-on intérêt à choisir une valeur de E ni trop élevée, ni trop faible.
E faible : mesure imprécise et trop petit nombre de mesure pour U.
U trop grand : effet Joule important dans les résistors.

On choisit E = 1,0512 V ( mesurée au voltmètre avec une précision de 0,3 mV) et R = 46,90 kW ( précision 40 W).
On mesure U = 0,7463 V ( précision 0,3 mV).
51. Estimer la valeur de la température T à laquelle la mesure a été effectuée.
R₀ = U R / (E-U) = 0,7463 x46,90 /(1,0512 -0,7463)=114,8 kW.

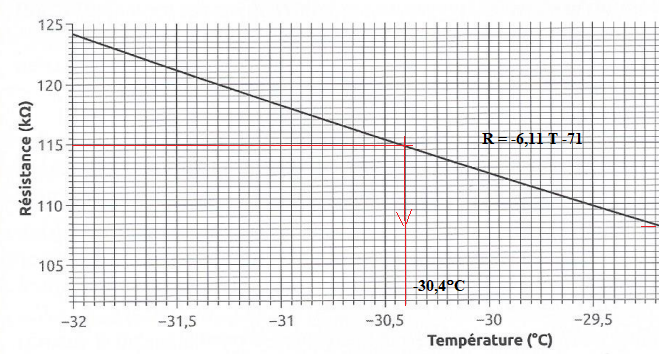
On cherche à estimer la valeur de l'incertitude-type u(T) dur la valeur de T.
On admet que si T = f(R₀), alors u(T) = |f '(R₀)| u(R₀) où u(R₀) est l'incertitude -type sur la valeur de R₀.
On cherche à obtenir une estimation de u(R₀) connaissant les précisions sur E, R et U.
52. Ecrire un script adapté qui estime l'incertitude-type u(R₀).
Import numpy as np
import numpy.random as rd
# valeur centrale de l'intervalle
m=-30,4
#précision
a = 0,2
# nombre de tirages
N=1000
# définition d'un tableau contenant N valeurs
# tirées aléatoirement dans l'intervalle [m-a ; m+a]
tab = rd.uniform(m-a, m+a, N)
# affichage de l'incertitude
print ('u(m)=',np.stb(tab, ddof=1))
Le script affiche u(R₀) = 1,3 10² ohms.
R₀= (114,8 ±0,13 kW.
53. En déduire une estimation de u(T)
u(T) = 6,11 x0,13 ~0,8 °C.

Analyse des profils de température.
Un échantillon parallélépipédique de neige de dimensions a x b x c est traversé par un flux thermique F selon l'axe Oz.
On note T(c) respectivement T(0) ) la température de l'interface neige-air à l'altitude c ( respectivement z = 0).

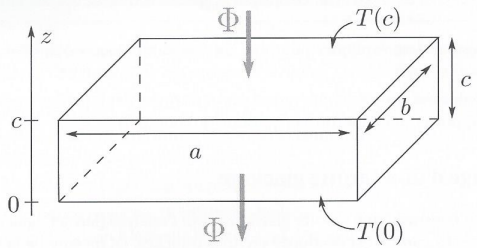
54. Rappeler la relation entre la résistance thermique R_th, la puissance F et les températures T(0) et T(c), puis l'expression de R_th en fonction des paramètres de l'échantillon et de la conductivité thermique de la neige.
R_th = [T(c)-T(0) ] / F.
R_th = c / (l ab).
55. Expliquer pourquoi plus la conductivité thermique d'un matériau est faible, plus il constitue un bon isolant thermique.
F = [T(c)-T(0) ] / R_th = [T(c)-T(0) ] ab l / c.
A [T(c)-T(0) ] ab / c constant, le flux thermique est d'autant plus faible que la conductivité thermique du matériau est plus petite.
56. Proposer une explication au caractère bon isolant thermique de la neige.
La neige est un mélange d'air et d'eau sous forme solide (glace) sous forme gazeuse. C'est un bon isolant thermique car elle contient une grande quantité d'air.
On effectue des mesures de températures dans un trou de forage juste après perçage en 2008 puis les mêmes mesures reproduites dans le même forage en 2009. On constate que les différences de températures sont très faibles.
A cause de sa faible conductivité thermique, la neige garde en mémoire la température qu'il faisait lorsqu'elle était à la surface. La température dans un trou de forage ne varie pas.
.